Понятие о годографе и кажущейся скорости.

Одним из стержневых понятий в теории сейсморазведки является понятие годографа.

Зная положение точек наблюдения, в которых определено время прихода волны, можно составить зависимость t = 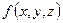.Зависимость времени прихода волны от координат точек наблюдения называют годографом.

Рассмотрим такую зависимость для прямой волны вдоль линии наблюдения OS лежащей на плоскости. На этой же плоскости находится источник колебаний (рис45).

Рис. 45. Поверхностный (а) и линейный (б) годографы прямой волны; поверхностные изохроны прямой волны (в)

Выберем систему координат так, чтобы начало ее находилось в точке возбуждения колебаний О. Рассматриваемая волна бежит вдоль поверхности от точки O к точке S, координаты которой x и y.

Отсюда

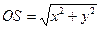, а уравнение времени записывают в виде .

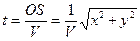Из аналитической геометрии следует, что это уравнение конуса вращения. Ось вращения – ось t. Вращением системы координат можно совместить ось x с OS. Тогда y под корнем исчезнет и уравнение будет приведено к виду 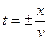. Это уравнение прямой, исходящей из начала координат. У нее две симметричные относительно оси t ветв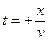и: и 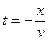. Такое уравнение называется линейным продольным годографом прямой волны(Рис.45б). Геометрически это сечение конуса вращения (пространственного годографа прямой волны) вертикальной плоскостью, проходящей через начало координат. Непродольный линейный годограф получим, если линия наблюдения не проходит через О. Он будет представлять собой результат вертикального сечения конуса плоскостью, не проходящей через начало координат. Как известно, такое сечение представляет собой гиперболу (рис45а). Здесь точка О' – проекция О на линию профиля l в плоскости XOY.С понятием годографа тесно связано понятие кажущейся скорости V^*

Поместим на линию наблюдений ОХ несколько сейсмоприемников и зарегистрируем с их помощью волну, годограф которой показан на рис.46. Допустим, что эта волна движется откуда-то из глубины и нам известно положение фронта волны, подошедшей к первому сейсмоприемнику, стоящему в точке Р₁. Угол падения волны на линию наблюдения обозначим i. Пусть также известна скорость распространения рассматриваемой волны – V и эта скорость постоянна. Тогда нетрудно получить, воспользовавшись принципом Гюйгенса-Френеля положение фронта волны в точке P₂ в момент времени t₂ = t₁ + Δt. За отрезок времени Δt волна пробежала путь ΔS по лучу К и можно записать, что Δt= 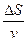. Из рисунка видно, что ΔS = Δхsini, поскольку ΔS -противолежащий углу i катет в образовавшемся на рис.46 прямоугольном треугольнике.

а

Рис.46. К выводу закона Бенндорфа.

Наблюдателю, находящемуся на поверхности, кажется, что волна, двигаясь от P₁ к P₂ преодолела расстояние Δх вдоль поверхности наблюдения со скоростью, равной

V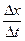^*= . Если устремить Δх к нулю, то есть перейти к бесконечно малым, то получим V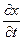^*= . Такая скорость называется кажущейся V^*. Это не скорость перемещения фронта волны, а скорость движения его проекции (его следа) вдоль линии наблюдения. Из приведенной геометрии видно, что связаны эти скорости через sin i, то есть

V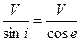^*= , где е – угол, дополняющий i до 90°. Такой угол называют углом выхода сейсмической радиации. Это выражение носит название закона кажущейся скорости или закона Бенндорфа.

Из сказанного видно, что V^* представляет собой дифференциальный параметр или производную годографа. Памятуя о геометрическом смысле производной (тангенс угла наклона касательной к кривой в точке, где мы хотим установить наклон этой кривой) уясним как измерить кажущуюся скорость по любому годографу, если он криволинеен: надо к точке, где мы хотим найти V^*, провести касательную и определить тангенс угла ее наклона Δх/Δt. Величина кажущейся скорости зависит от направления подхода волны к поверхности наблюдения( Рис.46,б)

Если эта волна движется вдоль поверхности наблюдения, то есть фронт волны перпендикулярен этой поверхности (α = 90°), то из выражения V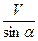^*= следует, что V^*= V (так как sin90°= 1). Так двигаются поверхностные волны-помехи и определенная по годографам этих волн V^* будет как угодно близка к истинной, составляющей в приповерхностной части разреза 500-1000 м/сек. Если же волны приходят снизу, по направлению близкому к вертикали (фронт волны практически параллелен поверхности наблюдения), то V^*→∞, поскольку α→0. Так двигаются полезные отраженные волны, откуда следует, что полезные волны те, которые имеют очень высокие кажущиеся скорости, превышающие, как правило, 5000 м/сек.

Сказанное означает, что можно по величинам кажущихся скоростей отделять полезные волны от помех, осуществлять их фильтрацию по кажущимся скоростям.

Проблема борьбы с помехами чрезвычайно актуальна и составляет главное содержание методики проведения полевых работ и обработки данных. Сами по себе возможности этой борьбы обусловлены тем, что каждая волна характеризуется своими кинематическими зависимостями, то есть формой годографа. Поэтому теория годографа - основной элемент теории сейсморазведки и исследователи заняты решением прямой и обратной кинематических задач сейсморазведки – получением уравнений годографов самых разных волн для самых разных моделей среды и исследованием этих уравнений. Уравнение годографа прямой волны мы уже рассмотрели выше. Остановимся теперь на годографах отраженных и преломленных волн. Для получения уравнения линейного продольного годографа в случае простейшей двухслойной модели среды обратимся к рис. 47.

Пусть произвольный луч падающей волны касается границы R в точке R. Из этой точки отражения исходит колебание по лучу RS под углом, равным углу падения (рассматривается монотипная волна). Таким образом, уравнение времени по рассмотренному лучу может быть записано в виде (Рис. 47б)

.

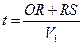Буквенную запись необходимо переписать так, чтобы это была зависимость t от х , и параметров модели среды: угла наклона границы, ее глубины и т.д.,. Для вывода уравнения воспользуемся методом зеркальных отображений и проведем ряд дополнительных построений. Рассматривается плоский (двумерный) случай, где все лучи принадлежат вертикальной плоскости, проходящей через профиль наблюдений. Так бывает, когда профиль разбит вкрест простирания пород и границы геологических напластований являются плоскими. Зависимость t(х) выводится в системе с общей точкой возбуждения (ОТВ) в центре расстановки сейсмоприемников (СП), когда колебания возбуждаются в одной точке О, а регистрация волн осуществляется сейсмоприемниками, расставленными по линии –х - +х, проходящей через точку О (продольный профиль).

Опустим из точки О нормаль на границу раздела R и продолжим за эту границу до пересечения с продолжением луча RS. Они пересекутся в точке О*, которая является зеркальным отображением О ( в зеркале границы R). Это можно доказать из рассмотрения треугольников ОRМ и О*RМ. Нетрудно показать, что они равны. Оба они прямоугольные, МR – общий катет, углы ОRМ и О*RМ равны, поскольку равны углу, дополняющему их до 90°. Следовательно равны катеты ОМ и О*М, представляющие глубину границы по нормали, и гипотенузы ОR и О*R. Таким образом, можно записать, что RS+ RO* = О*S, то есть можно представить лучи, исходящие из пункта возбуждения О через лучи, исходящие из О*. Точка О* называется поэтому мнимым пунктом возбуждения.

Итак, уравнение времени можно переписать в таком виде

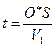
О*S является гипотенузой большого прямоугольного треугольника О*О'S, где О' – проекция точки О* на линию наблюдения. Следовательно О*S= .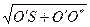

О'S можно представить как разность х (абсцисса точки S) и х₀=ОО'. ОО' – это противолежащий углу φ катет в узком вертикальном прямоугольном треугольнике О*О'O, откуда следует О'О=2h·sinφ. Угол О'О*О равен φ (углу наклона границы),так как это углы с взаимно-перпендикулярными сторонами. Координата точки О* по оси Z обозначена через Z. Тогда можно записать О*S= 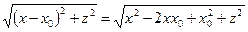. Поскольку 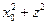из треугольника О*О'О равно 4h², выражение для АВ можно переписать так

О*В=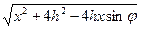

и уравнение годографа запишется в виде

t=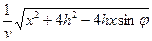

<26 27 282930 31 32 >

Дата добавления: 2017-01-26; просмотров: 3436;

Поиск по сайту

Узнать еще