Это уравнение гиперболы с минимумом над мнимым пунктом возбуждения.

Если положить х=0, то время t₀ над точкой возбуждения колебаний (началом координат) окажется равным

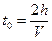
При горизонтальном залегании границы R, то есть при равенстве угла φ нулю уравнение годографа отраженной волны примет вид

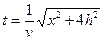
В этом случае точка минимума гиперболы окажется над пунктом возбуждения, тогда как при наклоне границы R она смещается в сторону восстания отражающей поверхности.

Поверхностный (пространственный) годограф ОВ нетрудно получить вращением гиперболы относительно вертикальной оси симметрии (параллельной оси времени), проходящей через точку О₁ (рис.47а). Полученная фигура называется гиперболоидом вращения.

Годограф преломленной волны в системе ОТВ также нетрудно вывести, однако мы дадим его запись в готовом виде, а тех, кто затрудняется сделать самостоятельный вывод, адресуем к учебникам в списке литературы.

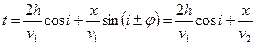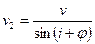, где в сторону падения границы, и 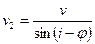в сторону ее восстания. V₂, то есть скорость скользящей вдоль границы преломленной волны будет равна кажущейся скорости, а кажущиеся скорости по восстанию и падению будут различаться. V₂ соответствует граничной скорости V_г если толща 2 однородная и изотропная, в противном случае V_г - как скорость движения волны вдоль напластования (волна бежит в одном и том же слое, подстилающем границу R) не совпадает с V₂ , характеризующей осредненные свойства среды 2. Приведенное выше уравнение показывает, что линейный продольный годограф преломленной волны представляет собой две прямолинейные ветви, которые будучи продолженными до пересечения с осью времени t пересекутся в одной точке t₀ (Рис 48).

Если преломляющую границу считать горизонтальной, то есть положить φ=0, годограф преломленной волны примет вид

Рис.48. Годограф головной (преломленной) волны (плоская преломляющая граница, однородная покрывающая среда)

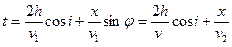
Геометрически это будут две симметричные ветви, исходящие из t₀ с одинаковыми значениями x начальных точек выхода и с одинаковыми значениями времени 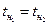в этих начальных точках.

В кинематической теории распространения волн рассматриваются и исследуются уравнения годографов всех перечисленных выше и иных волн, свидетельствующие об их существенных отличиях, что является основанием для выбора (селекции) этих волн, когда возникает такая необходимость. Определенные возможности такого выбора можно проиллюстрировать, рассмотрев вопрос о соотношении годографов основных типов волн, используемых в сейсморазведке: отраженных, преломленных и прямых все для той же простой двухслойной модели среды и для того же простого двумерного (плоского) случая. Для еще большей простоты положим, что отражающая (преломляющая) поверхность R горизонтальна (Рис.49 ).

Рис.49. Соотношение годографов основных типов волн.

Выпишем уравнения годографа всех трех, показанных на рис. 49 волн

1)

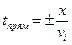
2)

3)

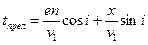
Чтобы уяснить соотношение годографов прямых и отраженных волн, устремим в выражении для t_отр х → ∞. Тогда любым конечным числом в том числе h (и 4h²) в сравнении с ∞ можно будет пренебречь. Следовательно t_{отр →} t_прям, откуда можно заключить, что на бесконечности эти годографы сходятся, неограниченно сближаются. То есть асимптотой годографа отраженной волны (гиперболы) является годограф простой волны (прямая). Такое соотношение называется асимптотическим приближением.

Чтобы уяснить соотношение годографов отраженной и преломленной волн, рассмотрим на рис.49 ситуацию вблизи падения волны под критическим углом. Очевидно, что последний докритический луч отраженной волны и самый первый луч головной практически совпадают (отличаются на бесконечно малую), значит и времена годографов отраженной и преломленной волны будут одинаковыми. Такой случай, когда кривая (гипербола – годограф ОВ) и прямая (годограф преломленной волны) имеют общую точку называется в геометрии касанием. Итак, годограф прямой волны в точке t_нач касается годографа ОВ. Наконец, соотношение годографов прямой и преломленной волн – пересечение. Именно так классифицируется случай, когда две прямые на плоскости(плоскости годографа х,t) имеют общую точку. Нетрудно определить координаты этой точки, для чего необходимо приравнять правые части уравнения 1 и 3 положив х = х₁.

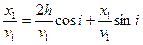, отсюда 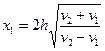, то есть точка пересечения лежит на расстоянии от начала координат как минимум в два раза большем, чем глубина h исследуемой границы раздела R. Какие же практические выводы можно сделать из рассмотренного соотношения годографов? Их три.

1) Область примыкающая к источнику (вплоть до места сближения годографов всех трех волн) – это область работ методом МОВ. Здесь регистрации отраженных волн не мешают головные (они регистрируются на бо'льших удалениях), а от прямых волн отраженные отделены достаточно большим промежутком времени Δt (если граница залегает на глубине более 200-300м) и прямые волны успевают уйти от регистрирующих приборов. При мелком залегании такого промежутка Δt не будет и отраженные волны не удастся проследить уверенно.

2) область больших удалений от источника (>2h) это пространство, благоприятное для применения МПВ, поскольку преломленные волны регистрируются здесь в первых вступлениях, то есть приходят раньше всех других видов колебаний. Известно, что одной из главных задач, для решения которой применяется методика МПВ, является картирование рельефа поверхности кристаллического фундамента платформенных территорий. Глубина залегания фундамента на территории Восточно-Европейской платформы обычно не превышает 2,5-3 км. Это значит, что для регистрации первых вступлений преломленных волн от поверхности фундамента надо уходить на расстояние более 6-7 км от источника. В то же время, в Прикаспийской впадине, где глубины залегания фундамента оцениваются в 20-25 км, удаление должно составить более 50 км.

3) В области, где сближаются годографы всех волн и регистрируется очень сложная их интерференция (наложение) заниматься сейсмической разведкой вообще не рекомендуется.

Таким образом, рассмотренный вопрос о соотношении годографов основных типов волн приобретает отчетливое методическое значение и практический смысл.