Поперечно-цилиндрическая проекция Гаусса. Плоская прямоугольная система координат

Решение геодезических задач в этой системе выполняется по простым формулам аналитической геометрии, для чего необходимо предварительно элементы поверхности эллипсоида тем или иным способом спроектировать на плоскость. Такое проецирование будет сопровождаться неизбежными искажениями, а их величина и характер зависят от вида выбранной поверхности.

Для крупномасштабного картографирования и инженерной геодезии наиболее удобны проекции, обеспечивающие наилучшее сохранение подобного изображения фигур при переходе от эллипсоида на плоскость. Это станет возможным, если земную поверхность разделить на части (зоны), а затем изобразить всю ее на плоскости. Возникающие при этом искажения будут малы и легко учитываться.

Таким требованиям отвечает принятая в СССР с 1928 года поперечно-цилиндрическая проекция Гаусса-Крюгера. Эту проекцию Гаусс предложил в 1825 – 1830 г.г., в 1912 году Крюгер разработал детали применения и дал рабочие формулы для вычислении в этой проекции.

Сущность проекции Гаусса-Крюгера заключается в следующем.[7]

Поверхность земного эллипсоида разбивают меридианами на сферические двуугольники – зоны через 60 (рис 6).

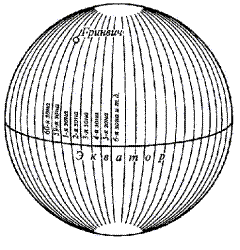
Рис. 6

Мысленно располагают такой эллипсоид в цилиндре так, чтобы осевой меридиан первой зоны касался боковой поверхности цилиндра (рис.7).

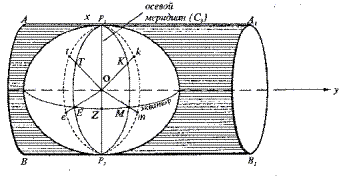
Рис. 7

Ось цилиндра «y» располагается поперек малой оси эллипсоида (поэтому проекция называется поперечно-цилиндрической), а ось «x», в отличие от математики, в геодезии располагается на север. Из центра эллипсоида все точки(T,E,Z,M,K… ) шестиградусной зоны проектируют по отвесным линиям на боковую поверхность цилиндра (t,e,Z,m,k…). Затем вращательно-поступательно перемещают эллипсоид в цилиндре таким образом, чтобы осевой меридиан второй зоны касался боковой поверхности цилиндра и все точки на граничных меридианах этой зоны проектируют аналогично. И так далее проектируют все 60 зон эллипсоида.

Разрезав цилиндр по образующим АА1 и ВВ1 и развернув половину его боковой поверхности, получают изображение земной поверхности на плоскости в виде отдельных зон, соприкасающихся одна с другой лишь в точках по экватору. (Рис. 8).

Ось цилиндра и линия экватора лежат в одной плоскости и после развертки изобразятся прямой линией - ось «y». Ось «x» располагается перпендикулярно оси «y», совпадает с осевым меридианом зоны и малой осью эллипсоида. Таким образом, осевой меридиан и экватор изображаются взаимно-перпендикулярными прямыми линиями. После развертки поверхности эллипсоида, спроектированной на боковую поверхность цилиндра, получаются разрывы земной поверхности, заметные в северном и южном полушариях по широте более 580 (рис.8). Шестиградусные зоны нумеруются арабскими цифрами с запада на восток, начиная от Гринвичского меридиана. Долготу осевого меридиана (0) любой зоны можно определить по формуле:

λ₀ = 6⁰N - 3⁰ (4)

где N - номер зоны.

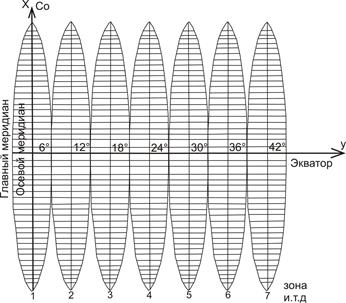
Рис.8

За начало счета координат в каждой зоне принимается пересечение изображений осевого меридиана – оси абсцисс «x» и экватора «y». Показанные на рис. 8 линии, параллельные изображению осевого меридиана (в нужной зоне) и экватора, образуют прямоугольную систему координат. Координаты (x и y) могут иметь знаки «+» и «-». Так как территория России расположена севернее экватора, то все «x» будут положительные; «y» – западнее осевого меридиана будут иметь отрицательные значения. Во избежание путаницы в знаках, то есть, чтобы ординаты были положительными, точкам осевого меридиана условно присваивается значение 500 км или осевой меридиан каждой зоны условно переносится на 500 км на запад (рис. 9).

Тогда ординаты получают условные значения и называются преобразованными у́_А, у́_Д . Впереди измененной ординаты записывается номер зоны, в которой находится данная точка.

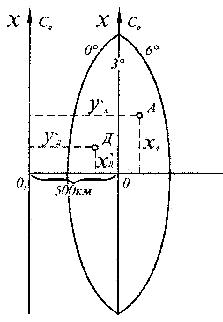
Рис. 9

§ 9. Зависимость между сферическими прямоугольными координатами эллипсоида и плоскими прямоугольными координатами в проекции Гаусса

Главные радиусы кривизны в данной точке эллипсоида.

Если бы Земля имела форму шара радиуса R, то кривизна ее поверхности во всех точках была бы постоянной и одинаковой, равной , а координаты любой точки на ее поверхности зависели бы от B и L (рис. 5).

В действительности, как было отмечено выше, Земля близка по форме к эллипсоиду вращения с разными размерами полуосей (§6). Таким образом, кривизна земной поверхности меняется от точки к точке, а значит координаты любой точки будут зависеть не только от B и L , но и от кривизны земной поверхности, то есть от главных радиусов кривизны эллипсоида [9].

Через нормаль к поверхности эллипсоида (рис. 5) можно провести бесчисленное множество плоскостей. Эти плоскости, перпендикулярные к касательной плоскости к поверхности эллипсоида в данной точке, называются нормальными. Кривые, образуемые от пересечения нормальных плоскостей, проведенных в данной точке, с поверхностью эллипсоида, называются нормальными сечениями. В каждой точке эллипсоида существуют два взаимно перпендикулярных нормальных сечения, кривизна которых имеет максимальное и минимальное значение; эти нормальные сечения называются главными нормальными сечениями.

В некоторой точке M (рис 10) поверхности земного эллипсоида главными нормальными сечениями, как известно из дифференциальной геометрии, являются:

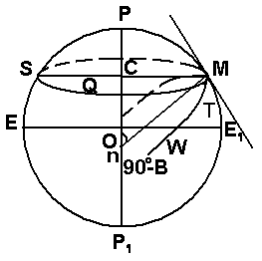
Рис.10

-меридианальное сечение, проходящее через данную точку M, и оба полюса эллипсоида P и P1 (на рис. 10 меридианальное сечение в точке M представляются эллипсом PME1P1E);

-сечение первого вертикала, проходящее через точку M и перпендикулярное меридианальному сечению точки M.

Сечение первого вертикала изображено на рис. 9 кривой WME, представляющей собой также эллипс. Обозначим через M и N радиус кривизны меридиана и первого вертикала и запишем соответственно [9]:

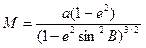(5)

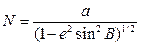(6)

где a – большая полуось эллипсоида;

e² – квадрат первого эксцентриситета меридианального сечения;

B - геодезическая широта точки M.

Зависимость между сфероидическими и плоскими прямоугольными координатами.

Точка A (рис. 11) на земном эллипсоиде имеет сферические координаты ХА , YА и расположена в 6-ти градусной зоне на некотором удалении (YА) от осевого меридиана.

Рис. 11

Так как по условию проекции осевой меридиан зоны касается боковой поверхности цилиндра, то после проектирования и развертки боковой поверхности цилиндра абсцисса ХА изобразится на плоскости величиной хА без искажений (рис. 12), то есть

х_А =Х_А (7)

Ордината YА получает искажение и после проектирования вычисляется по формуле:

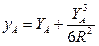(8)

Сферические прямоугольные координаты точки A находятся по формулам:

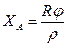(9)

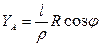(10)

где R – радиус кривизны Земли

φ – широта точки А

l – угловое расстояние точки A от осевого меридиана (разность долгот точки A и осевого меридиана);

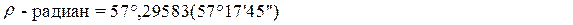
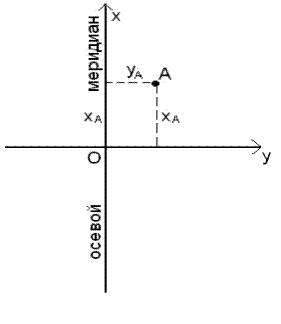
Рис. 12

Формулы 9 и 10 справедливы, если Землю принять за шар; в действительности же, мы знаем, Земля близка по форме к эллипсоиду вращения и зависимость между плоскими прямоугольными координатами и сфероидическими координатами намного сложнее.

В литературе [9] приводится сложный вывод этих формул, мы же ограничимся конечным результатом и запишем:

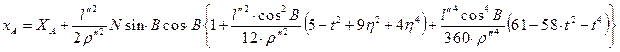(11)

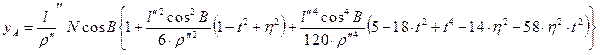(12)

где ĺ - длина дуги в секундах по параллели от осевого меридиана зоны до точки А; находится как разность долгот данной точки и осевого меридиана.

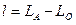(13)

В - геодезическая широта точки;

L_А - геодезическая долгота точки;

L_o - геодезическая долгота осевого меридиана зоны (находится по формуле 4);

N - радиус кривизны первого вертикала (берется из таблицы [5]; или выполняется по формуле 6);

ХА - приближенная абсцисса точки (берется из таблицы [5]);

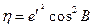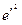; = 0,0067385

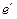- второй эксцентриситет меридианного эллипса