Сведения о фигуре Земли

Физическая поверхность Земли, являющаяся сочетанием материков и водных пространств, в геометрическом отношении представляет собой сложную форму, ее нельзя представить ни одной из известных и математически изученных геометрических фигур. На ней моря и океаны занимают около 71 %. а суша около 29 %. Если поверхность океанов и соединяющихся с ними морей почти почти ровная, то их дно и суша представляет разнообразные сочетания поверхностей - возвышенностей и углублений.

Если бы Земля находилась в неподвижном состоянии, представляла бы однородное тело, подвергалась бы только действию внутренних сил тяготения, ела бы форму шара. А так как Земля вращается вокруг своей оси с постоянной скоростью, то под действием центробежной силы она приняла форму сфероида или эллипсоида вращения, представляющего тело, полученное от вращения эллипса вокруг его малой оси.

Изучением формы и размеров Земли занимается наука «Высшая геодезия».

Задачи высшей геодезии подразделяются на научные и научно- технические.

Главной научной задачей высшей геодезии является изучение фигуры (т.е. формы и размеров) и внешнего гравитационного поля Земли. Решение этой задачи включает:

1) определение вида и размеров математически правильной поверхности, достаточно хорошо представляющей фигуру Земли в целом. Такой поверхностью признается поверхность эллипсоида вращения с малым сжатием; он называется земным эллипсоидом. Определение поверхности земного эллипсоида заключается в установлении параметров, характеризующих его размер, форму и расположение (ориентирование ) в теле Земли.

2) изучение действительной формы Земли и ее внешнего гравитационного поля. Под действительной фигурой Земли понимается реальная физическая поверхность. Изучение действительной фигуры Земли заключается в определении геометрических величин, характеризующих отступление ее поверхности от поверхности установленного земного эллипсоида.

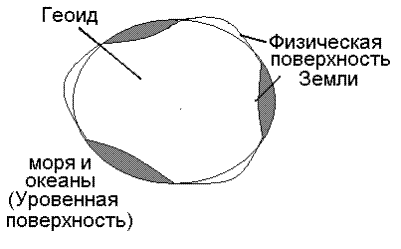
Рис. 2

Если уровень морей и океанов в их спокойном состоянии мысленно продолжить под материки (Рис. 2), то образуется тело – геоид, близкое к форме Земли («гео» - земля; «ид» - подобие), но поверхность геоида не имеет математического выражения. Исходя из этого за математическую фигуру Земли принят Земной эллипсоид, имеющий небольшие отступления от поверхности геоида (Рис. 3)

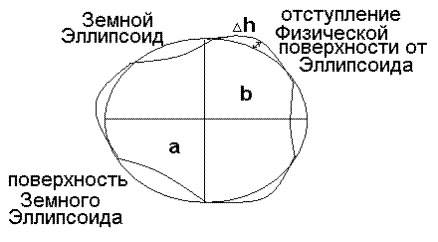
Рис. 3

Внешнее гравитационное поле Земли изучают по такому же принципу, как и фигуру Земли: сначала определяют гравитационное поле тела, близкого к Земле, за которое также принимается эллипсоид вращения, затем определяют отступление гравитационного поля реальной Земли от гравитационного поля выбранного эллипсоида.

Гравитационное поле Земли и фигура Земли неразрывно связаны между собой, и их изучение представляет собой одну задачу. Практически задача изучения фигуры Земли сводится к определению координат точек ее поверхности в единой, общей для всей Земли, системе, а задача изучения внешнего гравитационного поля Земли - к определению потенциала силы тяжести на поверхности Земли в ее внешнем пространстве в той же координатной системе. Под фигурой Земли понимается поверхность геоида. Геоид - тело, образованное уровенной поверхностью, совпадающей в океане с невозмущенной поверхностью воды, мысленно продолженной под материки таким образом, что направления отвесных линий пересекают эту поверхность во всех ее точках под прямым углом.[9]. Эта уровенная поверхность является непрерывной, замкнутой, всегда выпуклой. Поскольку фигура геоида зависит от неизвестного поля распределения масс внутри Земли, то она, строго говоря, неопределима. Это было показано советским ученым М.С.Молоденским, предложившим основной задачей геодезии считать изучение фигуры Земли на основании выполненных на земной поверхности измерений без привлечения каких-либо гипотез о внутреннем ее строении.

В теории М.С.Молоденского вводится вспомогательная поверхность квазигеоида, совпадающая с геоидом на океанах и морях и весьма мало отступающая от поверхности геоида на суше (менее 2 метров).

Вывод параметров земного эллипсоида производится под условием возможной его близости к квазигеоиду. Поверхность квазигеоида играет роль «уровня моря» и от нее ведется счет топографических высот. Таким образом, вместо изучения поверхности геоида, теория М.C. Молоденского требует определения фигуры квазигеоида. Но если ранее изучение фигуры геоида ставилась как основная задача геодезии, не получавшая точного и строгого решения, то поверхность квазигеоида вводится лишь как вспомогательная и точно определяется. По теории М.C. Молоденского все геодезические задачи получают строгое решение и необходимости в изучении фигуры геоида не возникает.

Изучение фигуры Земли представляет одну из важнейших проблем естествознания; знание форм и размеров Земли представляет большой научный и практический интерес не только для геодезии, но и для многих смежных наук – астрономии, геологии, географии и др.

Для решения многочисленных практических задач геодезии в конечном счете необходимы координаты отдельных точек земной поверхности в выбранной системе. Эти координаты непосредственно из измерений не определяются, а получаются из вычислений по результатам измерений. Но для вычисления координат точек земной поверхности и других ее элементов - площадей отдельных фигур, расстояний, направлений, разностей высот между заданными пунктами, и решения других геодезических задач по результатам непосредственных измерений необходимо знание этой поверхности, то есть ее формы и размеров. Однако, физическая поверхность Земли крайне сложна и использовать эту поверхность при математическом решении геодезических задач невозможно. Поэтому при решении математических задач геодезии используют поверхность эллипсоида (выражаемую простым уравнением), решение задач на которой уже не представляет трудностей. Желательно весьма, чтобы эллипсоид имел наибольшую близость к фигуре Земли в целом. Такой эллипсоид называется обычным земным эллипсоидом и определяется следующими условиями:

1. совпадение центра эллипсоида с центром тяжести Земли и плоскости его экватора с плоскостью земного экватора:

2. минимум суммы квадратов отклонений по высоте квазигеоида во всех его точках от поверхности эллипсоида.

В отдельных странах (или группе стран) применяются при обработке геодезических измерений эллипсоиды, выведенные по результатам геодезических работ, охватывающих территорию данной страны (или части ее) или нескольких стран. Такие «рабочие» эллипсоиды называются референц – эллипсоидами. Референц – эллипсоиды отличаются от общего земного эллипсоида. Это различие заключается в несовпадении размеров и центров с размерами и центрами общего земного эллипсоида, а условие минимума суммы квадратов отклонений выполняется для референц – эллипсоида не для всей поверхности Земли, а только для той части, на которой были выполнены геодезические работы, результаты которых использованы для вывода его параметров. Поэтому референц – эллипсоид можно рассматривать как эллипсоид, подходящий только для части поверхности Земли. Вследствие несовпадения центров референц – эллипсоида и реальной Земли, малая ось референц – эллипсоида не совпадает с осью вращения Земли, но параллельна последней; также не совпадают, а параллельны плоскости их экваторов. С какой бы степенью точности не были определены параметры референц – эллипсоида, его поверхность никогда не совпадет с поверхностью Земли или геоида (квазигеоида). Расстояние между поверхностями земного эллипсоида и геоида (квазигеоида) достигают в отдельных местах - 150 метров, а высота точек земной поверхности относительно эллипсоида – сотен и тысяч метров. Поэтому при математической обработке геодезических измерений просто «заменить» земную поверхность эллипсоидом нельзя, необходимо результаты измерений, выполненных на земной поверхности, предварительно спроектировать на поверхность эллипсоида путем введения соответствующих поправок за переход. «Отнесенные» таким образом величины - результаты непосредственных геодезических измерений – на поверхность эллипсоида уже можно подвергать строгой математической обработке, используя зависимости, существующие между отдельными элементами поверхности эллипсоида. Поэтому такие эллипсоиды и называются референц – эллипсоидами и эллипсоидами относимости. Такие эллипсоиды служат координатной поверхностью, на которой решаются геодезические задачи и относительно которых определяются геодезические координаты пунктов. Геодезические координаты определяются направлением нормалей к поверхности эллипсоида.