Масштабы топграфических карт

Помня приведенную выше ормулровку понятия карта, (уменьшенное изображение), перейдем к понятию масштаб карты

Под масштабом понимается число, показывающее во сколько раз линия на карте меньше своей горизонтальной проекции на местности. Поясним это на рис. 15 и 16.

На местности (рис.15) расстояние D между точками A и B измерено. Измерен так же угол наклона n местности (линии АВ) к горизонту (к уровенной поверхности).

d - горизонтальное проложение линии АВ (или проекция ее) вычисляется по формуле (16)

d = D * cos n (16)

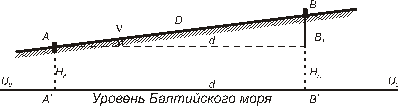
Рис.15.

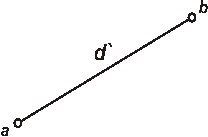
Рис.16

Точки А́ и В́- ортогональные проекции точек А и В на уровенную поверхность (уровень Балтийского моря).

Для построения линии АВ на плоскости бумаги (карты) надо ее проекцию (d) уменьшить в определенное число раз. Пусть линия А́В́(d) нанесена на карту по координатам ее концов (точек А́ и В́) и на рис.16 она обозначена через d́ Тогда по аналогии (4) запишем

d́/d = 1/(d/d́) = 1/M, (17)

d = d́ * M (18)

Предположим, что уменьшение произведено в 10 тыс. раз, т.е. масштаб карты 1:10000. Это означает, что в 1 см карты (линии на карте) содержится 10000 см горизонтальной проекции (d) этой линии на местности, а именно:

1 см — 10000 см,

или 1 см — 100 м.

Величину М в формуле 10 называют знаменателем масштаба.

Чтобы определить длину проекции линии на местности (18) сначала измеряют ее длину в сантиметрах по карте, а затем умножают на знаменатель масштаба. Наклонная же длина линии (D) на местности будет вычислена по формуле

D = d / cos n, (19)

получаемой из решения прямоугольного треугольника АВВ1 (рис.15).

Угол наклона n может быть вычислен по выражениям

tgn = h / d, (20)

n = arctg(h / d), (21)

где h - превышение между точками A и B, вычисляемое как

h = H_В – H_А; (22)

здесь H_А и H_В - абсолютные отметки точек A и B, или высоты этих точек над уровнем Балтийского моря.

Угол наклона n может быть вычислен по графику “Масштаб заложений для углов наклона”, изображенному на карте

Масштаб указывается под южной рамкой листа карты. Масштабы бывают: численный, именованный, линейный и поперечный.

Численный масштаб выражается дробью, числитель которой - единица, а знаменатель - число, показывающее во сколько раз произведено уменьшение.

Например, численный масштаб 1:25000 означает, что 1 см линии на карте соответствует 25000 см горизонтальной проекции этой линии на местности. Чем больше знаменатель, тем больше уменьшение длин, тем мельче изображение объектов на карте, т.е. мельче масштаб карты.

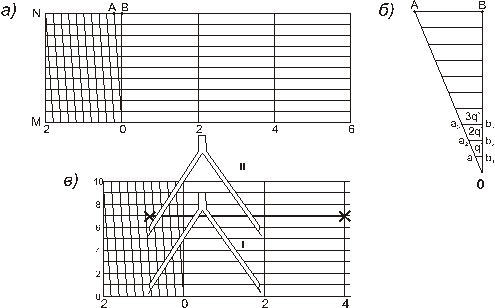
Рис.17.

Именованный масштаб — словесное пояснение соотношений длин линий на карте и на местности. Например для численного масштаба карты - 1:25000 “именованный” записывается так: в 1 сантиметре 250 метров.

Линейный масштаб изображается в виде линии (рис. 18), разделенной на 2 или 1 см (основание масштаба); левый крайний отрезок делится на 20 (10) частей; отрезки от нуля подписываются применительно к масштабу. Линейный масштаб позволяет определять с помощью измерителя значительно точнее длину линии на местности, не производя математических расчетов, как это делается при численном масштабе.

Поперечный масштаб (рис.17). Для повышения точности измерений применяют поперечный масштаб, который строится в виде прямоугольника длиной 8-10 см и высотой 2-3 см.

По длине прямоугольник разбивается вертикальными линиями через 2 см - основание масштаба (q); по высоте прямоугольник делится на 10 частей проведением горизонтальных линий.

Крайняя левая часть масштаба по линиям MO и NВ делится обычно на 10 равных частей (дробная часть основания), а точки деления вверху и внизу соединяются наклонными линиями (трансверсалями). В результате такого построения отрезки прямых между перпендикуляром ОВ и первой трансверсалью будут различной длины. Самый малый из них а1b1=q’ является наименьшим делением поперечного масштаба (рис. 17 б). Его величину можно определить на основании свойства подобных треугольников. Количество делений катета ОB равно 10. Следовательно, отрезок Оb1 составляет 1/10 катета ОВ. Учитывая, что треугольники OАВ и Oa1b1 подобны, тогда a1b1=0,1 АВ. Из этого же условия a2b2 =0,2 АВ и.т.д. А так как AB=0,1q,, то a1b1=0,01q.

Длину измеряемого с помощью поперечного масштаба отрезка (d) можно определить по выражению

d=(nq+m0,1q+k0,01q)M

где n – количество целых оснований (q);

m – количество полных десятых долей (q);

к – количество сотых делений основания (q);

М – знаменатель масштаба;

q – основание поперечного масштаба (1 или 2 см.).

Применительно к длине отрезка , обозначенного раствором измерителя, (положение I), если принять масштаб 1:50000 будем иметь: q=2см; M=500м.; n=1; m=3; k=5;

d=(1 х 2+0,1 х 2+5 х 0,01 х 2) х 500=1350м.

На практике все получается значительно проще. Измеритель, с установленным по карте раствором, переносят на нижнюю линию масштаба так, что бы одна его игла совместилась с одним из перпендикуляров справа от нулевой отметки, а другая оказалась в пределах крайнего левого основания (рис.17). Затем измеритель перемещают вверх до тех пор, пока левая игла не совпадёт с пересечением одной из наклонных линий с горизонтальной прямой, при этом обе иглы должны быть на одной горизонтальной прямой. Теперь достаточно подсчитать количество оснований (q), оно равно единице; количество десятых долей основания (0,1q) оно равно 3; количество сотых долей основания (0,01q), оно равно 5 и вычислить длину. Отрезка например, применительно к численному масштабу 1:50000 основание масштаба (q) равно 2 см, а в масштабе это 1000м, одно деление дробного основания – 100метров (в положении II таких делений 7) плюс 300 м; ножки измерителя находятся на 5 линии, плюс отрезок 5 х 0,01 х 1000=50м. Таким образом, полная длина отрезка равна 1000+ 300 + 50 = 1350 метров. Аналогично определяется длина линии, выделенная жирным тоном на поперечном масштабе. Ее длина равна 2 х 1000 х 3 х 100 х 7 х 10=2370м.