Геодезическая система координат

Координатными плоскостями, т.е. плоскостями, относительно которых определяют координаты точек пространства, являются плоскость экватора и земного эллипсоида и плоскость, меридиана, принятого за начальный. Плоскость экватора проходит через центр эллипсоида ”0” перпендикулярно его оси вращения РР1. Плоскость, проходящая через нормаль (Mn) к поверхности эллипсоида в данной точке и параллельная его малой оси “b” называется плоскостью меридиана этой точки. В качестве начального принят меридиан, плоскоть которого проходит через центр Гринвичской обсерватории, находящейся вблизи Лондона.

Координатными линиями являются меридианы и параллели.

Меридиан - это линия пересечения поверхности земного эллипсоида и меридианной плоскости.

Параллель - это линия пересечения поверхности земного эллипсоида и плоскости, проходящей через данную точку и параллельной плоскости экватора.

Пусть на рис. 5 РЕР1Е1 меридианный эллипс, проходящий через точку начала счета долгот (Гринвич), РMRP1 - меридиан, проходящий через данную точку М.

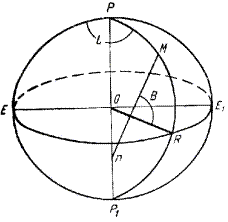
Рис. 5

Геодезической широтой точки M называется острый угол B, образованный нормалью Mn к поверхности эллипсоида в данной точке и плоскостью экватора ERE1.

Геодезической долготой L точки M будем называть двугранный угол, образованный плоскостью меридиана, PMP1 , проходящего через данную точку и плоскостью начального меридиана (он лежит в плоскости экватора ЕОR).

Широта B и долгота L вполне определяют положение точки M на поверхности эллипсоида.

Система геодезических координат находит широкое применение в теоретических выводах и вычислениях как научного, так и практического характера. Эта система имеет ряд достоинств:

а) едина для всей поверхности эллипсоида и, таким образом, объединяет в общий для всей земной поверхности координатной системе геодезические, съемочные и картографические материалы;

б) не требует каких-либо дополнительных и вспомогательных построений. Координатные линии в этой системе - меридианы и параллели непосредственно относятся к поверхности эллипсоида и их использование для составления карт и объединения всех картографических съемочных материалов в единое целое удобно даже в том случае, если территория этих съемок не представляет сплошного массива;

в) определяет положение нормалей к поверхности принятого референц-эллипсоида, что весьма важно и удобно при исследовании фигуры Земли, определении уклонений отвесных линий и проведении других исследований научного и практического характера. [16].

Геодезические координаты относятся к математически правильной поверхности эллипсоида вращения, принимаемого при геодезических вычислениях, в отличие от астрономических широт и долгот, которые относятся к уровенной поверхности. Если геодезическую широту мы определяем как угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора, то астрономическую широту мы определяем как угол между отвесной линией в данной точке и плоскостью экватора; соответственно астрономической долготой называется двугранный угол, образованный между плоскостью нулевого меридиана и плоскостью астрономического меридиана данной точки (плоскость астрономического меридиана – плоскость, проходящая через отвесную линию в этой точке и параллельная оси вращения Земли).

В геодезических работах различиями между астрономическими и геодезическими координатами никогда не пренебрегают; более того эти различия, вызываемые уклонениями отвесных линий выбором размеров референц-эллипсоида и ориентировки его, являются предметом особого изучения.

В мелкомаштабных картографических работах различиями между астрономическими и геодезическими координатами при известных условиях можно пренебречь и употреблять широты и долготы как координаты общей системы географических координат.

Однако, применение геодезических координат для практических целей сопряжено с рядом трудностей, а именно:

1) положение пунктов определяется в угловых единицах, в то время как все расстояния на местности вычисляются (или измеряются) в линейной мере;

2) значение одних и тех же угловых единиц соответствует разным линейным величинам в зависимости от широты;

3) использование геодезических координат связано со сложными вычислениями. [16]

Таким образом, возникла необходимость выбора такой координатной системы, которая по простоте и удобству использования могла бы найти применение во всех геодезических работах. Такой системой является система плоских прямоугольных координат в проекции Гаусса.