Частотные критерии устойчивости

По виду частотных характеристик САУ можно судить об устойчивости систем, поэтому существуют частотные критерии устойчивости систем, которые позволяют осуществлять исследование устойчивости систем во взаимосвязи с графическим представлением их характеристик.

Частотные критерии имеют довольно простую интерпретацию, поэтому с их помощью удобно исследовать устойчивость систем, описываемых характеристическими уравнениями высокого порядка.

Рассмотрим основные критерии.

Критерий Михайлова

В 1938 году русский ученый А.В.Михайлов сформулировал критерий устойчивости САУ, основанный на анализе годографа Михайлова и принципе аргумента, которым обусловлено, что сумма аргументов всех сомножителей комплексного числа равна аргументу произведения комплексных чисел.

Возьмем характеристическое уравнение системы следующего вида:

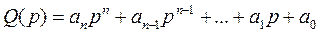(2.43.)

Подставим в уравнение мнимое значение р = jw и получим:

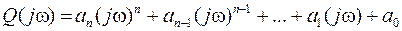(2.44.)

Полученное выражение представляет собой математическое описание вектора Михайлова, конец которого при изменении частоты w от 0 до ¥, будет описывать на комплексной плоскости кривую, называемую годографом Михайлова, графическое представление которого изображено на рисунке 68.

Критерий Михайлова сформулирован следующим образом: САУ является устойчивой, если годограф Михайлова при изменении частоты от0 до ¥ начинается приw = 0на положительной вещественной полуоси, и с увеличением частоты проходит в положительном направлении (против часовой стрелки) последовательно, нигде не обращаясь в нуль,nквадрантов координатной плоскости, гдеnявляется порядком характеристического уравнения системы.

Система является неустойчивой при любом отклонении от критерия Михайлова. На рисунке 68 годограф 1 соответствует устойчивой системе, описываемой уравнением 3-го порядка, годограф 2 соответствует устойчивой системе, описываемой уравнением 4-го порядка, годограф 3 соответствует неустойчивой системе, годограф 4 соответствует системе, находящейся на границе устойчивости, при этом годограф Михайлова проходит через 0.

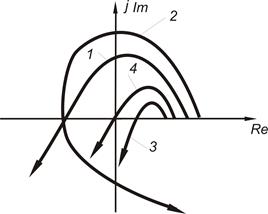
Рис.68. Графическое представление годографа Михайлова

1 и 2 – устойчивая система, 3 – неустойчивая система,

4 – система находится на границе устойчивости

На рисунке 69 изображены годографы Михайлова для устойчивых и неустойчивых систем, где n - порядок дифференциального уравнения:

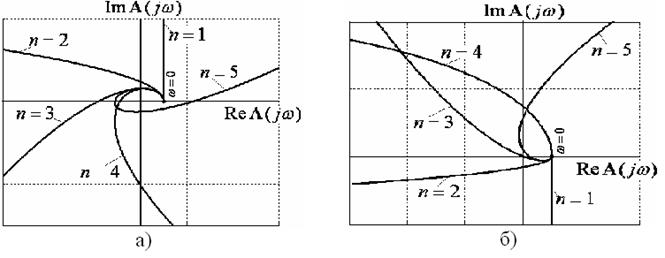
Рис.69. Годографы Михайлова:

а) устойчивых систем, б) неустойчивых систем