Пример определения устойчивости САУ с помощью критерия Михайлова
Необходимо определить устойчивость САУ, структурная схема которой представлена на рисунке 65, числовые значения данных представлены в таблице на рисунке 66.
Решение:
Характеристическое уравнение данной системы имеет вид:
D(s) = 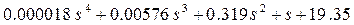 (2.42.)
(2.42.)
Подставив в уравнение 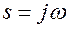 , получим:
, получим:
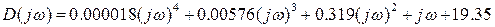 (2.45.)
(2.45.)
Преобразуем уравнение в следующий вид:
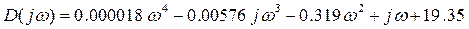 (2.46.)
(2.46.)
Выделим действительную и мнимую части:
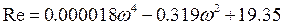 ;
; 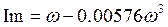 (2.47.)
(2.47.)
Для построения годографа Михайлова составим таблицу значений (рисунок 70):
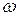
| 7.817 | 13.176 | 132.9 | 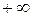
| |
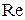
| 19.35 | −35.49 | 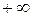
| ||
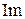
| 5.0654 | −13386.75 | 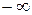
|
Рис.70. Таблица значений
С помощью таблицы значений построим на комплексной плоскости годограф Михайлова и представим его на рисунке 71.
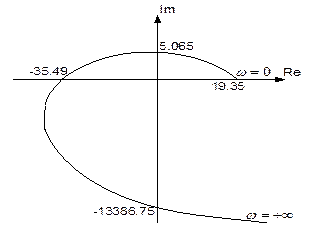
Рис.71. Годограф Михайлова
Анализируя годограф на рисунке 71 в соответствии с критерием Михайлова можно сделать вывод, что САУ устойчива, т.к. годограф начинается на действительной оси и с ростом ω от 0 до 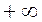 обходит последовательно в положительном направлении 4 квадранта комплексной плоскости.
обходит последовательно в положительном направлении 4 квадранта комплексной плоскости.
Критерий Найквиста
В 1932 г. американский физик Найквист сформулировал критерий устойчивости САУ, позволяющий судить об устойчивости замкнутой системы по АФЧХ ее разомкнутого контура. Критерий Найквиста сформулирован следующим образом – если САУ устойчива в разомкнутом состоянии, то необходимым и достаточным условием ее устойчивости в замкнутом состоянии будет условие, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до+ ¥ не охватывала на комплексной плоскости точку с координатами (-1; j0).
Из определения разомкнутой системы вытекает, что входная величина системы является входной величиной первого звена прямой цепи, а выходной величиной разомкнутой системы является выходная величина последнего звена цепи обратной связи. Для замкнутой системы передаточная функция разомкнутой системы примет следующий вид:
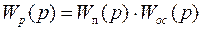 (2.48.)
(2.48.)
Заменив в формуле передаточной функции разомкнутой системы (2.48.)
р = jw, получим АФЧХ разомкнутой системы n - ного порядка:
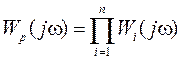 (2.49.)
(2.49.)
Указанную АФЧХ разомкнутой системы построим на комплексной плоскости при увеличении частоты от 0до +¥, что показано на рисунке 72.
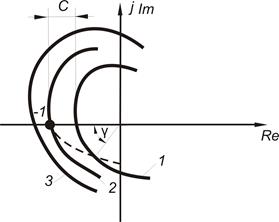
Рис.72. Критерий устойчивости Найквиста:
1 – АФЧХ устойчивой системы, 2 – АФЧХ системы на границе
устойчивости, 3 – АФЧХ неустойчивой системы
В случае, когда АФЧХ разомкнутой системы пройдет через точку с координатами
(-1; j0), как видно из рисунка 72 (график 2), система будет находиться на колебательной границе устойчивости. В случае, когда АФЧХ разомкнутой системы будет охватывать точку с координатами (-1; j0), замкнутая система будет являться неустойчивой (рисунок 72, график 3).
Дата добавления: 2017-01-26; просмотров: 6589;











