Интеграл с переменным верхним пределом
Заметим, что в качестве переменной интегрирования можно выбрать любую букву:
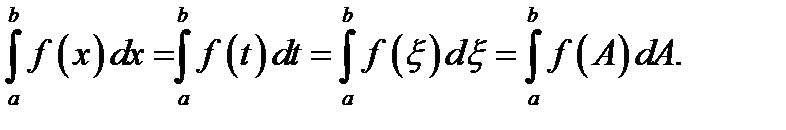
Пусть функция 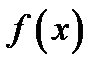 интегрируема на отрезке
интегрируема на отрезке 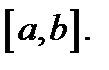 Тогда для любого
Тогда для любого 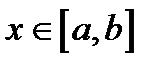 можно вычислить число
можно вычислить число 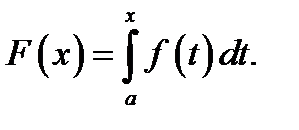 Значит, для каждого
Значит, для каждого 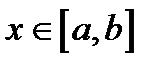 определена функция
определена функция 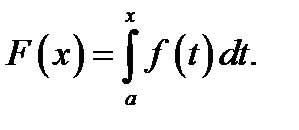 Эту функцию называют интегралом с переменным верхним пределом.
Эту функцию называют интегралом с переменным верхним пределом.
Теорема 1.Если функция 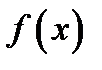 интегрируема на отрезке
интегрируема на отрезке 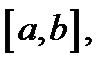 то интеграл
то интеграл 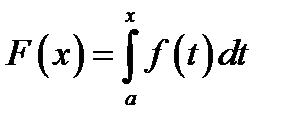 непрерывен на этом отрезке. Если
непрерывен на этом отрезке. Если 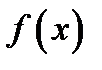 непрерывна на отрезке
непрерывна на отрезке 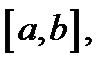 то
то
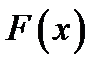 дифференцируема на указанном отрезке, причем
дифференцируема на указанном отрезке, причем
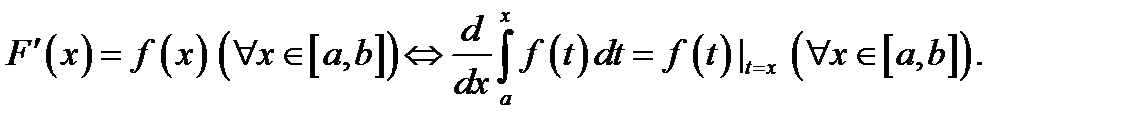
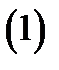
Доказательствопервой части этого утверждения опускаем. Перейдем к обоснованию второй части. Пусть 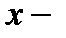 произвольная точка интервала
произвольная точка интервала 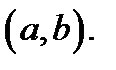 Вычислим
Вычислим
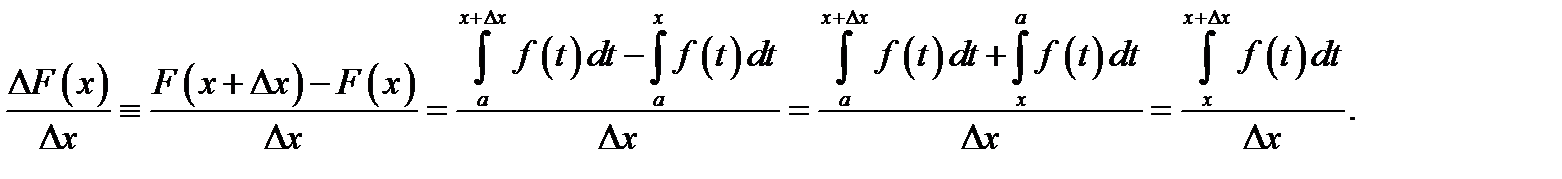
Так как 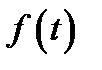 непрерывна на отрезке
непрерывна на отрезке 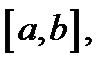 то применима теорема о среднем: существует точка
то применима теорема о среднем: существует точка 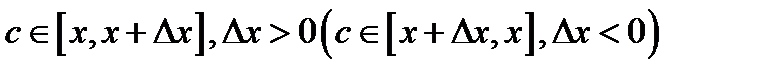 такая, что
такая, что
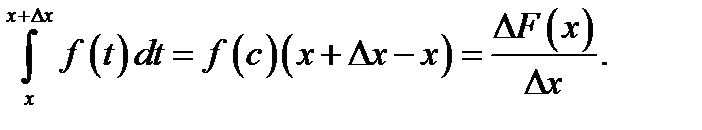
Тогда 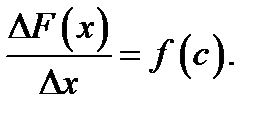 Устремляя здесь
Устремляя здесь 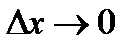 и учитывая, что при этом
и учитывая, что при этом 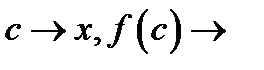
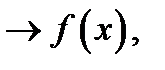
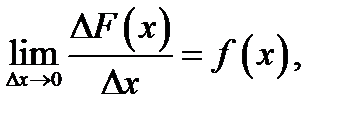 т.е.
т.е. 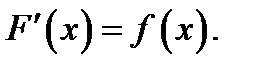 Равенство (1) показано в любой внутренней точке отрезка
Равенство (1) показано в любой внутренней точке отрезка 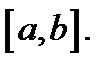 Можно показать, что оно верно и на концах этого отрезка. Теорема доказана.
Можно показать, что оно верно и на концах этого отрезка. Теорема доказана.
Следствие 1.Любая непрерывная на отрезке 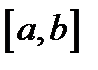 функция
функция 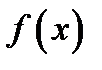 имеет первообразную.
имеет первообразную.
Действительно, в качестве одной из первообразных можно указать интеграл 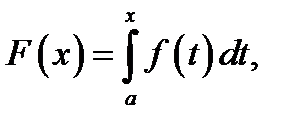 с переменным верхним пределом (
с переменным верхним пределом ( 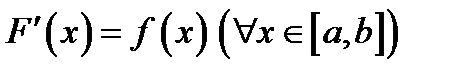 ).
).
Дата добавления: 2016-06-05; просмотров: 1522;











