Техническая интерпретация

Логических функций

По логическим выражениям проектируются схемы ЭВМ. При этом надо придерживаться определенной последовательности действий.

1. Словесное описание работы схемы.

2. Формализация словесного описания.

3. Запись функций в дизъюнктивной (конъюнктивной) совершенной нормальной форме по таблицам истинности.

4. Минимизация логических зависимостей с целью их упрощения.

5. Представление полученных выражений в выбранном логически полном базисе элементарных функций.

6. Построение схемы устройства.

7. Проверка работоспособности полученной схемы. Покажем взаимосвязь перечисленных этапов на примере.

Пример 2.16.Спроектировать схему, фиксирующую появление «неправильной» тетрады в двоично-десятичном представлении чисел.

1. Каждая тетрада двоично-десятичного представления числа содержит десятичные цифры 0—9, что соответствует двоичным числам 0000—1001. Значения тетрады, соответствующие двоичным числам 1010—1111 (шестнадцатеричные цифры А—F), не должны появляться при представлении десятичных чисел.

2. Составим таблицу истинности функции (табл. 2.8), которая принимает значения, равные единице, при появлении «неправильных» тетрад. Разряды тетрады обозначим переменными х, у, z, и.

Таблица 2.8 Таблица истинности функции F

3. Исходная совершенная дизъюнктивная нормальная форма записы вается как

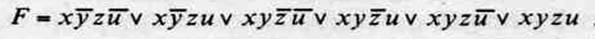
4. Эта форма функции допускает упрощение, что видно по диаграмме Вейча (табл.2.9). Этот же результат может быть получен аналитически.

Таблица 2.9 Диаграмма Вейча для функции F

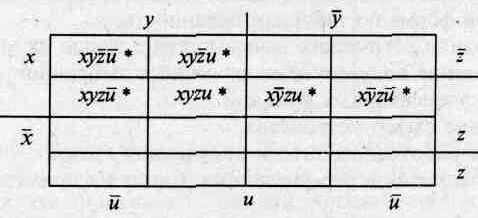
5. Минимальная форма функции F в логически полном базисе {&, v, [} будет иметь вид:

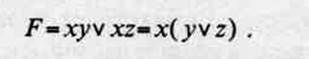
Для представления этой же схемы в другом полном базисе, например {& }, воспользуемся правилом де Моргана:

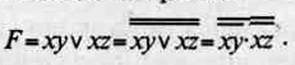
6. По полученным зависимостям можно построить схемы фиксации «неправильных» тетрад (рис. 2.2).

7. Проверить работоспособность построенных схем можно путем задания различных комбинаций переменных х, у, z, и и определения реакции на выходе схемы F.

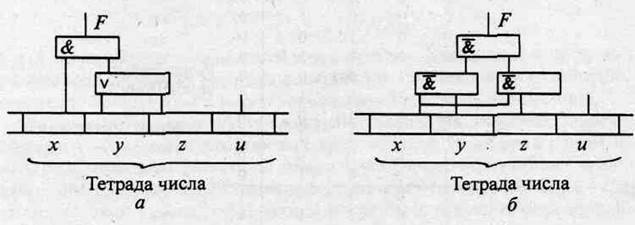
Рис. 2.2. Схема фиксации «неправильных» тетрад:

а — схема в базисе ( [, &, v),

б — схема в базисе (&)

<5 6 7 8 9 1011>

Дата добавления: 2017-01-26; просмотров: 953;