Понятие о минимизации логических функций

<5 6 7 8 91011 >

Проблема минимизации логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них оптимальной (минимальной). Существует большое количество методов минимизации ЛФ. Все они отличаются друг от друга спецификой применения операций склеивания и поглощения, а также различными способами сокращения переборов. Среди аналитических методов наиболее известным является метод Квайна — МакКласки, среди табличных — метод с применением диаграмм Вейча [6]. Графические методы минимизации отличаются большей наглядностью и меньшей трудоемкостью, однако их применение эффективно при малом числе переменных n≤5.

Рассмотрим последовательность действий минимизации ЛФ на примере.

Пример 2.15.Найти минимальную дизъюнктивную форму функции, заданной таблицей истинности (табл. 2.6).

Таблица 2.6 Таблица истинности функцииУ=f(x₁, x₂, x₃)

Х₁	Х₂	X_з	Y

Эта функция интересна тем, что имеет несколько минимальных форм. По данным таблицы запишем аналитическое выражение: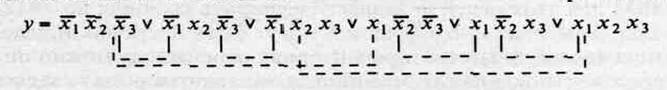

Пунктирными линиями в этом выражении отмечены пары конъюнкций, к которым можно применить операцию склеивания типаFx V Fx =F. Особенно хорошо это видно при использовании диаграммы Вейча, в которой «склеиваемые» конъюнкции находятся по соседству друг с другом. Диаграмма Вейча просто по-другому интерпретирует таблицу истинности (табл. 2.7).

Та б л и ц а 2.7 Диаграмма Вейча функции у

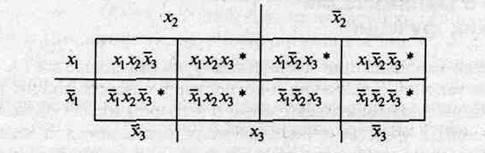
После выделения конъюнкций (они отмечены звездочкой), видно, какие конъюнкции могут образовывать пары для склеивания.

В результате применения операций склеивания и поглощения можно получить другое аналитическое выражение:

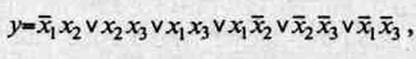
в котором отсутствуют возможности дальнейших склеиваний и поглощений. Однако последнее выражение является избыточным, так как отдельные конъюнкции могут быть «лишними», т.е. их «составные части» могут включаться в другие конъюнкции. У данной функции существует пять безызбыточных дизъюнктивных форм, из которых только две являются минимальными:

Из приведенных зависимостей видно, что только функции у₁ и у₄являются минимальными формами функций, так как они содержат наименьшее число конъюнкций и имеют минимальный ранг этих конъюнкций.

Минимизация «вручную» возможна только для функций, зависящих от 4—5 переменных, так как трудоемкость переборов растет в квадратичной зависимости от числа переменных. Применение мощных ЭВМ для этих целей позволяет расширить границы до n=12—15. Если при этом учесть, что функции могут быть частично определены (значения функций на некоторых наборах переменных можно определять произвольно), а также, что иногда приходится решать задачи совместной минимизации систем ЛФ, то минимизация ЛФ становится сложной инженерной, практической и научной проблемой.

<5 6 7 8 91011 >

Дата добавления: 2017-01-26; просмотров: 1471;