Контрольная работа №3
Дифференциальное исчисление функций нескольких переменных
Задание 1. Дана функция z=z(x; y), точкаА(x0; y0) и вектор а. Найти производную в точке А в направление вектора ā.
1.1. 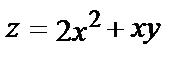
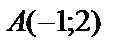
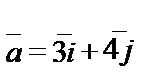 .
.
1) 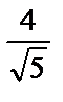 ; 2)
; 2) 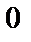 ; 3)
; 3) 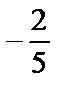 ; 4)
; 4) 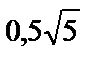 ; 5)
; 5) 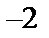 .
.
1.2. 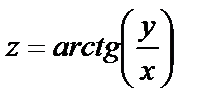
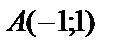
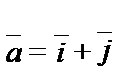 .
.
1) 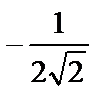 ; 2)
; 2) 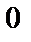 ; 3)
; 3) 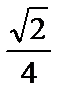 ; 4)
; 4) 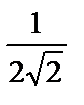 ; 5)
; 5) 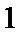 .
.
1.3. 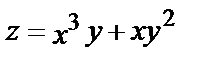
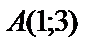
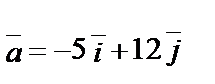 .
.
1) 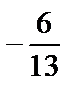 ; 2)
; 2) 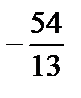 ; 3)
; 3) 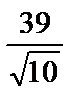 ; 4)
; 4) 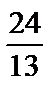 ; 5)
; 5) 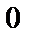 .
.
1.4. 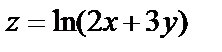
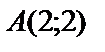
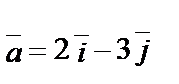 .
.
1) 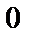 ; 2)
; 2) 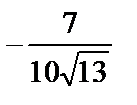 ; 3)
; 3) 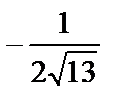 ; 4)
; 4) 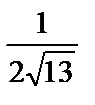 ; 5)
; 5) 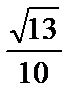 .
.
1.5. 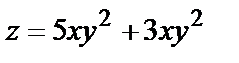
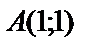
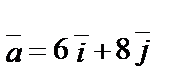 .
.
1) 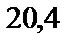 ; 2)
; 2) 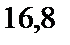 ; 3)
; 3) 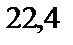 ; 4)
; 4) 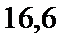 ; 5)
; 5) 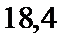 .
.
1.6. 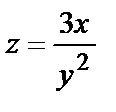
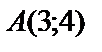
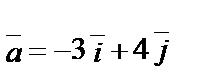 .
.
1) 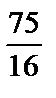 ; 2)
; 2) 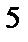 ; 3)
; 3) 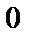 ; 4)
; 4) 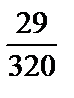 ; 5)
; 5) 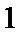 .
.
1.7. 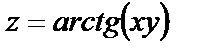
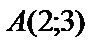
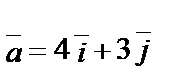 .
.
1) 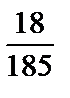 ; 2)
; 2) 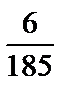 ; 3)
; 3) 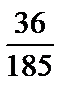 ; 4)
; 4) 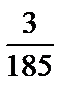 ; 5)
; 5) 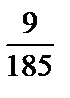 .
.
1.8. 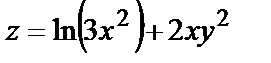
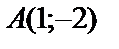
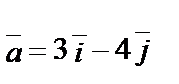 .
.
1) 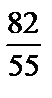 ; 2)
; 2) 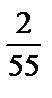 ; 3)
; 3) 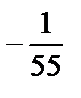 ; 4)
; 4) 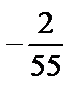 ; 5)
; 5) 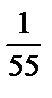 .
.
1.9. 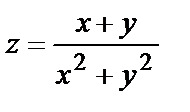
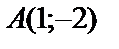
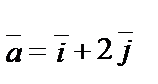 .
.
1) 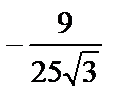 ; 2)
; 2) 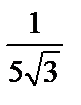 ; 3)
; 3)  ; 4)
; 4) 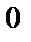 ; 5)
; 5) 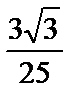 .
.
1.10. 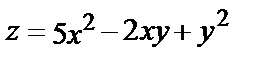
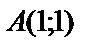
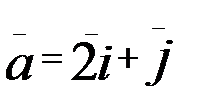 .
.
1) 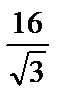 ; 2)
; 2) 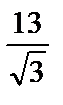 ; 3)
; 3) 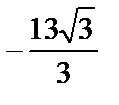 ; 4)
; 4) 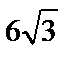 ; 5)
; 5) 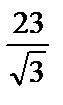 .
.
1.11. z=x2+xy+y2 A(1;1), 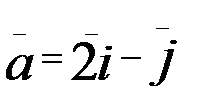 .
.
1.12. z=2x2+3xy+y2 A(2;1), 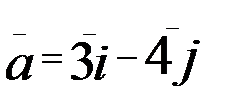 .
.
1.13. z=In(5x2+3y2); A(1;1), 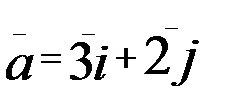 .
.
1.14. z=In(5x2+4y2); A(1;1), 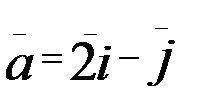 .
.
1.15. z=5x2+6xy; A(2;1), 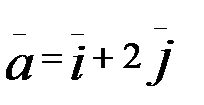 .
.
Задание 2. Вычислить приближенно.
2.1. 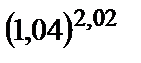
1) 1,08; 2) 1,1; 3) 1,06; 4) 1,04; 5) 1.
2.2. 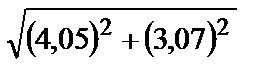
1) 5,082; 2) 5,012; 3) 5,08; 4) 5,146; 5) 5,041.
2.3. 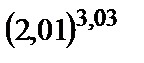
1) 8,36; 2) 8,32; 3) 8,29; 4) 8,44; 5) 8,25.
2.4. 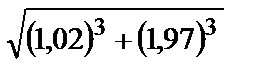
1) 2,99; 2) 3,01; 3) 2,94; 4) 3,084; 5) 3.
2.5 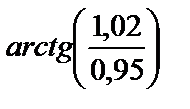
1) 0,785; 2) 0,81; 3) 0,81; 4) 0,775; 5) 0,8.
2.6. 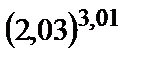
1) 8,31; 2) 8,43; 3) 8,42; 4) 8,44; 5) 8,32.
2.7 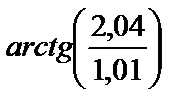
1) 63,36; 2) 1,117; 3) 1,111; 4) 1,129; 5) 1,107.
2.8. 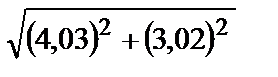
1) 5,2; 2) 5,03; 3) 5,036; 4) 5,01; 5) 5,04.
2.9 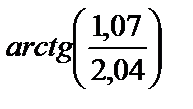
1) 0,488; 2) 0,464; 3) 0,440; 4) 0,552; 5) 0,562.
2.10. 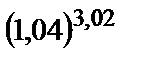
1) 1,01; 2) 1,04; 3) 1,06; 4) 1,14; 5) 5,12.
2.11. 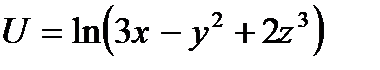
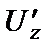 в точке М (1; 0; 1) равно ...
в точке М (1; 0; 1) равно ...
1) 5 2)3 3)1/5 4) 6/5 5)1/3
2.12. 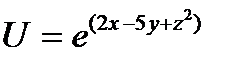
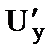 в точке M(0;-1;1) равно ...
в точке M(0;-1;1) равно ...
1) e6 2)5e6 3) -e6 4) -5e6 5) e
2)
2.13. 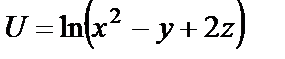
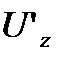 в точке M (1;2;2) равно ...
в точке M (1;2;2) равно ...
1) 2/3 2)3/2 3)-1/3 4)0 5)–2
2)
2.14. 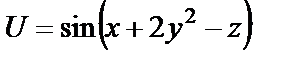
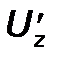 в точке
в точке 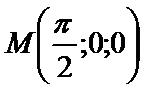 равно...
равно...
1) 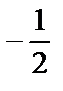 2)
2) 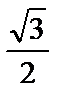 3) 0 4) 1 5)
3) 0 4) 1 5) 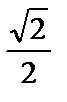
2.15. U= cos(x2-y+z3) U¢y в точке M (0;-p/2;0) равно ...
1) 1 2) 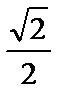 3) 0 4)-
3) 0 4)- 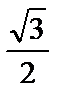 5)
5) 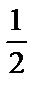
Задание 3.
Вычислите следующие интегралы:
3.1.1. 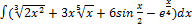 3.1.9.
3.1.9. 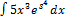
3.1.2. 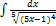 3.1.10.
3.1.10. 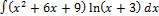
3.1.3. 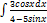 3.1.11.
3.1.11. 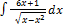
3.1.4. 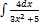 3.1.12.
3.1.12. 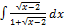
3.1.5. 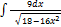 3.1.13.
3.1.13. 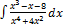
3.1.6. 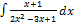 3.1.14.
3.1.14. 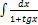
3.1.7. 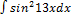 3.1.15.
3.1.15. 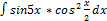
3.1.8. 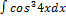
Вычислите следующие интегралы:
3.2.1. 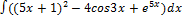 3.2.9.
3.2.9. 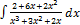
3.2.2. 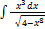 3.2.10.
3.2.10. 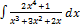
3.2.3. 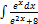 3.2.11.
3.2.11. 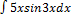
3.2.4. 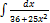 3.2.12.
3.2.12. 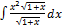
3.2.5. 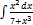 3.2.13.
3.2.13. 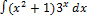
3.2.6. 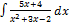 3.2.14.
3.2.14. 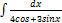
3.2.7. 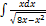 3.2.15.
3.2.15. 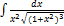
3.2.8. 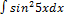
Вычислите следующие интегралы:
3.3.1. 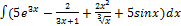 3.3.9.
3.3.9. 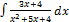
3.3.2. 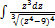 3.3.10.
3.3.10. 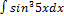
3.3.3. 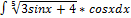 3.3.11.
3.3.11. 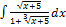
3.3.4. 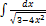 3.3.12.
3.3.12. 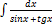
3.3.5. 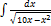 3.3.13.
3.3.13. 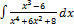
3.3.6. 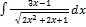 3.3.14.
3.3.14. 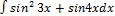
3.3.7. 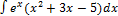 . 3.3.15.
. 3.3.15. 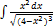
3.3.8. 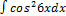
Вычислите следующие интегралы:
3.4.1. 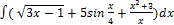 3.4.9.
3.4.9. 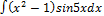
3.4.2. 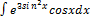 3.4.10.
3.4.10. 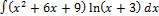
3.4.3. 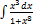 3.4.11.
3.4.11. 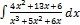
3.4.4. 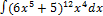 3.4.12.
3.4.12. 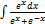
3.4.5. 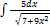 3.4.13.
3.4.13. 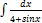
3.4.6. 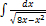 3.4.14.
3.4.14. 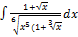
3.4.7. 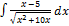 3.4.15.
3.4.15. 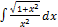
3.4.8. 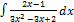
Вычислите следующие интегралы:
3.5.1. 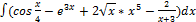 3.5.9.
3.5.9. 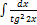
3.5.2. 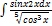 3.5.10.
3.5.10. 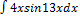
3.5.3. 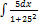 3.5.11.
3.5.11. 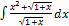
3.5.4. 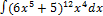 3.5.12.
3.5.12. 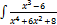 dx
dx
3.5.5. 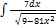 3.5.13.
3.5.13. 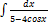
3.5.6. 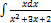 3.5.14.
3.5.14. 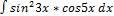
3.5.7. 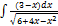 3.5.15.
3.5.15. 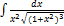
3.5.8. 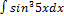
Вычислите следующие интегралы:
3.6.1. 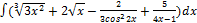 3.6. 9.
3.6. 9. 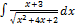
3.6.2. 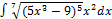 3.6. 10.
3.6. 10. 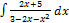
3.6.3. 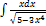 3.6.11.
3.6.11. 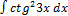
3.6.4. 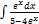 3.6. 12.
3.6. 12. 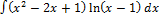
3.6.5. 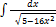 3.6.13.
3.6.13. 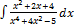
3.6.6. 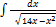 3.6. 14.
3.6. 14. 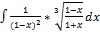
3.6.7. 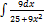 3.6. 15.
3.6. 15. 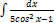
3.6.8. 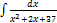
Вычислите следующие интегралы:
3.7.1. 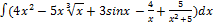 3.7. 9.
3.7. 9. 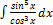
3.7.2. 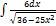 3.7.10.
3.7.10. 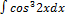
3.7.3. 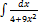 3.7.11.
3.7.11. 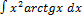
3.7.4. 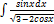 3.7.12.
3.7.12. 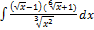
3.7.5. 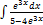 3.7.13.
3.7.13. 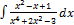
3.7.6. 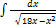 3.7.14.
3.7.14. 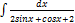
3.7.7. 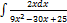 3.7.15.
3.7.15. 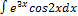
3.7.8. 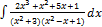
Вычислите следующие интегралы:
3.8.1. 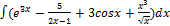 3.8.9.
3.8.9. 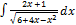
3.8.2. 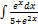 3.8.10.
3.8.10. 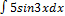
3.8.3. 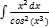 3.8.11.
3.8.11. 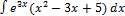
3.8.4. 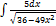 3.8.12.
3.8.12. 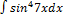
3.8.5. 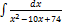 3.8.13.
3.8.13. 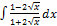
3.8.6. 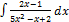 3.8.14.
3.8.14. 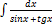
3.8.7. 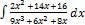 3.8.15.
3.8.15. 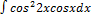
3.8.8. 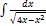
Вычислите следующие интегралы:
3.9.1. 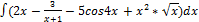 3.9. 9.
3.9. 9. 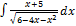
3.9.2. 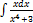 3.9.10.
3.9.10. 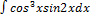
3.9.3. 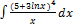 3.9.11.
3.9.11. 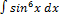
3.9.4. 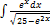 3.9.12.
3.9.12. 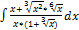
3.9.5. 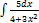 3.9.13.
3.9.13. 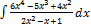
3.9.6. 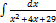 3.9.14.
3.9.14. 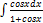
3.9.7. 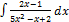 3.9.15.
3.9.15. 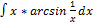
3.9.8. 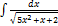
Вычислите следующие интегралы:
3.10.1. 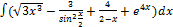 3.10.9.
3.10.9. 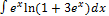
3.10.2. 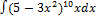 3.10.10.
3.10.10. 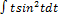
3.10.3. 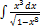 3.10.11.
3.10.11. 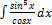
3.10.4. 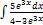 3.10.12.
3.10.12. 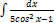
3.10.5. 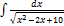 3.10.13.
3.10.13. 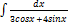
3.10.6. 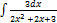 3.10.14.
3.10.14. 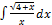
3.10.7. 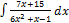 3.10.15.
3.10.15. 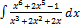
3.10.8. 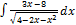
Вычислите следующие интегралы:
3.11.1. 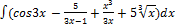 3.11.9.
3.11.9. 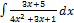
3.11.2. 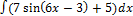 3.11.10.
3.11.10. 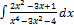
3.11.3. 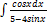 3.11.11.
3.11.11. 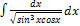
3.11.4. 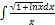 3.11.12.
3.11.12. 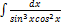
3.11.5. 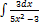 3.11.13.
3.11.13. 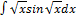
3.11.6. 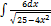 3.11. 14.
3.11. 14. 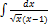
3.11.7. 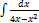 3.11.15.
3.11.15. 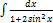
3.11.8. 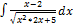
Вычислите следующие интегралы:
3.12.1. 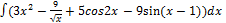 3.12.9.
3.12.9. 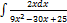
3.12.2. 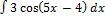 3.12.10.
3.12.10. 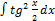
3.12.3. 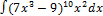 3.12.11.
3.12.11. 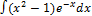
3.12.4. 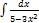 3.12.12.
3.12.12. 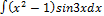
3.12.5. 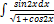 3.12.13.
3.12.13. 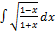
3.12.6. 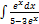 3.12.14.
3.12.14. 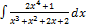
3.12.7. 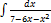 3.12. 15.
3.12. 15. 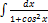
3.12.8. 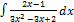
Вычислите следующие интегралы:
3.13.1. 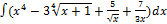 3.13. 9.
3.13. 9. 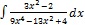
3.13.2. 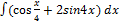 3.13.10.
3.13.10. 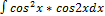
3.13.3. 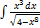 3.13.11.
3.13.11. 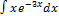
3.13.4. 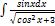 3.13.12.
3.13.12. 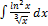
3.13.5. 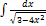 3.13.13.
3.13.13. 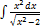
3.13.6. 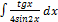 3.13.14.
3.13.14. 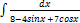
3.13.7. 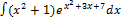 3.13.15.
3.13.15. 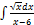
3.13.8. 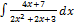
Вычислите следующие интегралы:
3.14.1. 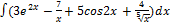 3.14.9.
3.14.9. 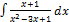
3.14.2. 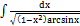 3.14.10.
3.14.10. 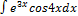
3.14.3. 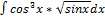 3.14.11.
3.14.11. 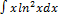
3.14.4. 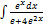 3.14.12.
3.14.12. 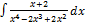
3.14.5. 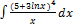 3.14.13.
3.14.13. 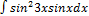
3.14.6. 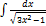 3.14. 14.
3.14. 14. 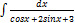
3.14.7. 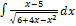 3.14.15.
3.14.15. 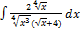
3.14.8. 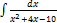
Вычислите следующие интегралы:
3.15.1. 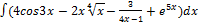 3.15. 9.
3.15. 9. 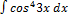
3.15.2. 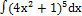 3.15.10.
3.15.10. 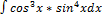
3.15.3. 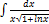 3.15.11.
3.15.11. 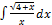
3.15.4. 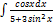 3.15.12.
3.15.12. 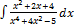
3.15.5. 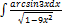 3.15.13.
3.15.13. 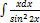
3.15.6. 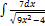 3.15.14.
3.15.14. 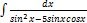
3.15.7. 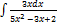
3.15. 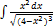
3.15.8. 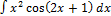
Задание 4. Вычислить (внесение функции под знак дифференциала).
4.1. 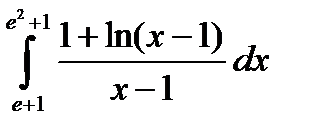
4.2. 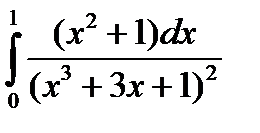
4.3. 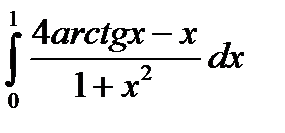
4.4. 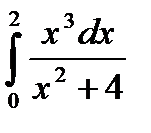
4.5. 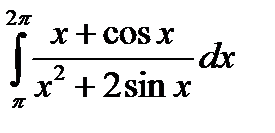
4.6. 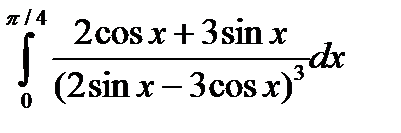
4.7. 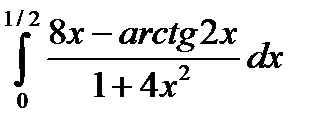
4.8. 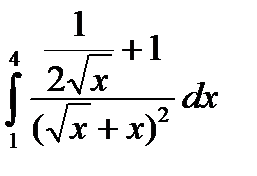
4.9. 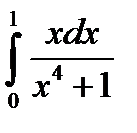
4.10. 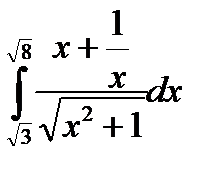
4.11. 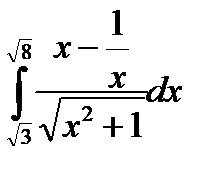
4.12. 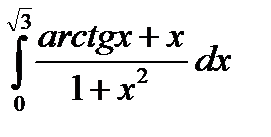
4.13. 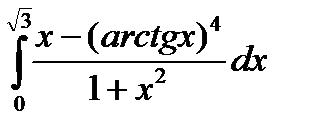
4.14. 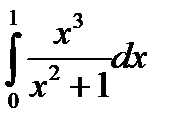
4.15. 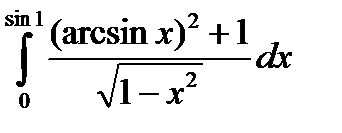
Задание 5.Вычислить применением метода интегрирования по частям.
5.1. 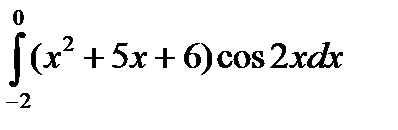
5.2. 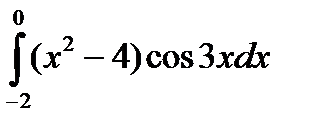
5.3. 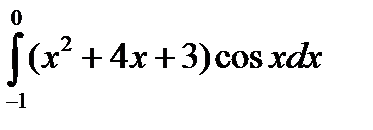
5.4. 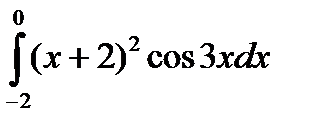
5.5. 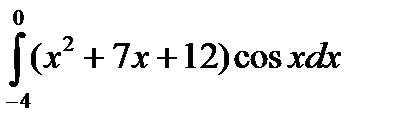
5.6. 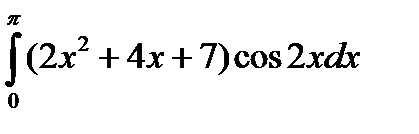
5.7. 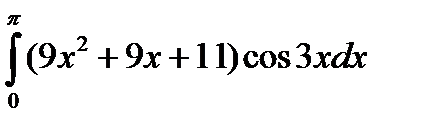
5.8. 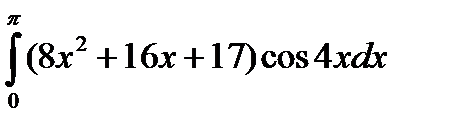
5.9. 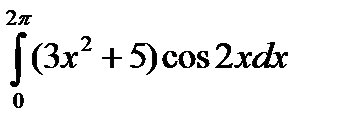
5.10. 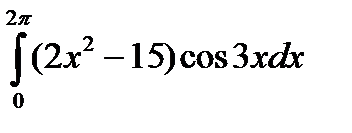
5.11. 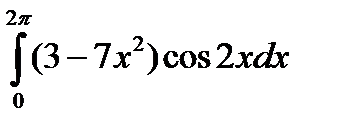
5.12. 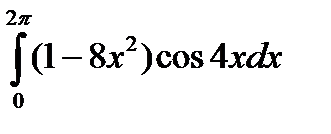
5.13. 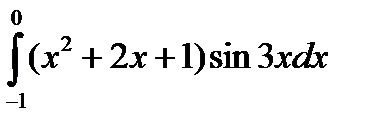
5.14. 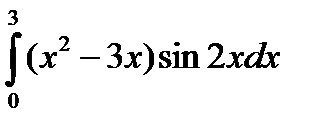
5.15. 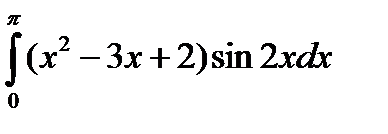
Задание 6. Вычислить универсальной подстановкой.
6.1. 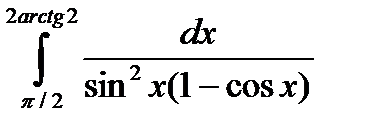
6.2. 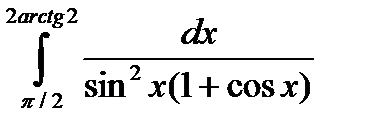
6.3. 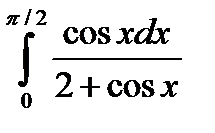
6.4. 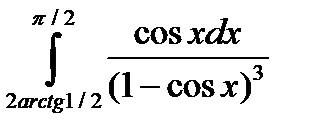
6.5. 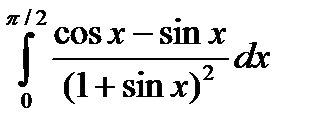
6.6. 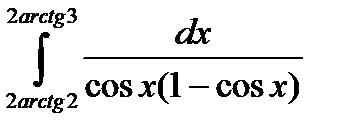
6.7. 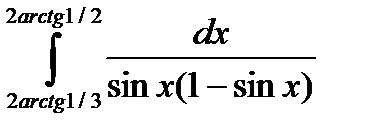
6.8. 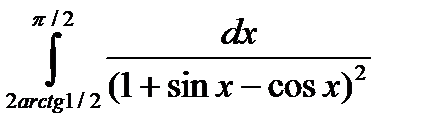
6.9 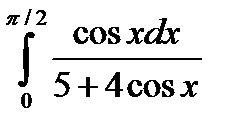
6.10. 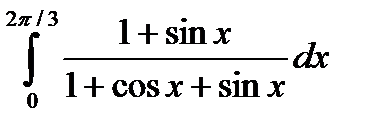
6.11. 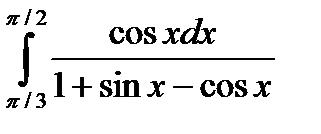
6.12. 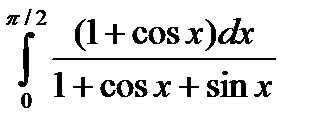
6.13. 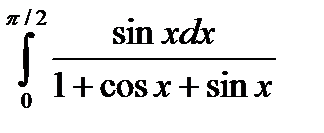
6.14. 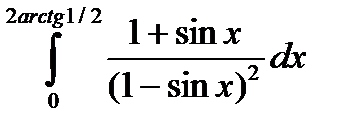
6.15. 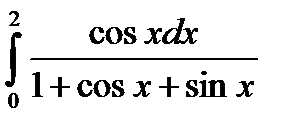
Задача 7. (подстановкой)
7.1. 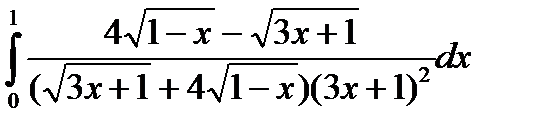
7.2. 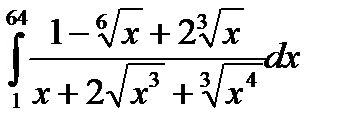
7.3. 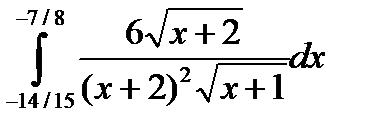
7.4. 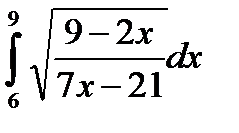
7.5. 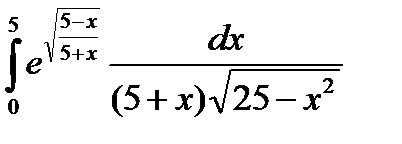
7.6. 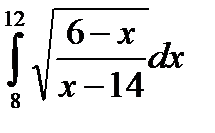
7.7. 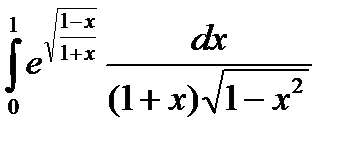
7.8. 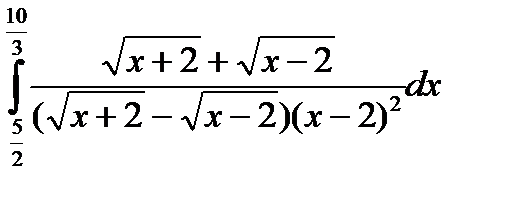
7.9. 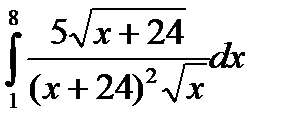
7.10. 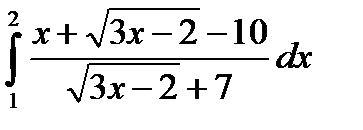
7.11. 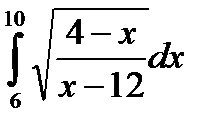
7.12. 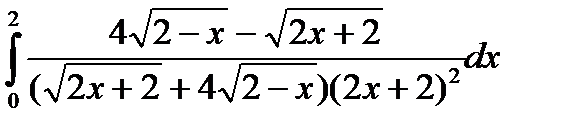
7.13. 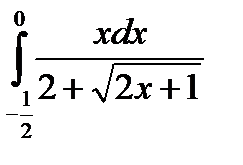
7.14. 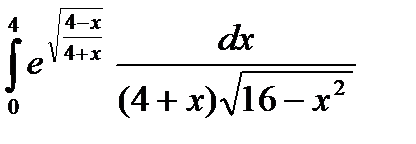
7.15. 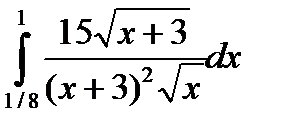
Задание 8.
Вычислить площадь плоской фигуры.
8.1Вычислить площадь фигуры, ограниченной кривой 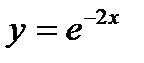 , прямыми х=-0,5, х=1 и осью абсцисс.
, прямыми х=-0,5, х=1 и осью абсцисс.
8.2Найти площадь фигуры, ограниченной кривой 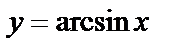 , прямыми
, прямыми 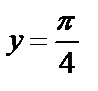 ,
, 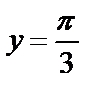 и осью ординат.
и осью ординат.
8.3Найти площадь фигуры, заключенной между окружностью 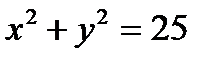 и прямыми 2у-5=0,
и прямыми 2у-5=0, 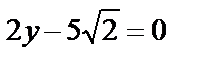
8.4Найти площадь фигуры, ограниченной эллипсом 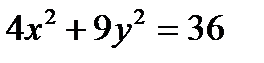 , прямой
, прямой 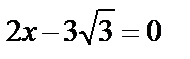 и осью ординат.
и осью ординат.
8.5Найти площадь фигуры, ограниченной ветвью гиперболы 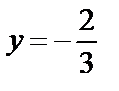 и прямыми х=1; х=5.
и прямыми х=1; х=5.
8.6Вычислить площадь фигуры, ограниченной кривой 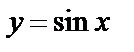 и осью абсцисс от
и осью абсцисс от 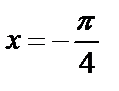 до
до 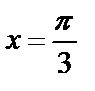 .
.
8.7 Найти площадь фигуры, ограниченной кривой 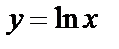 , прямыми
, прямыми 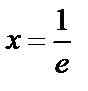 , х=е и осью абсцисс.
, х=е и осью абсцисс.
8.8 Вычислить площадь фигуры, ограниченной параболой 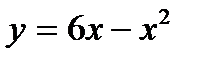 , прямыми х=-1, х=3 и осью абсцисс.
, прямыми х=-1, х=3 и осью абсцисс.
8.9 Найти площадь фигуры, ограниченной параболой 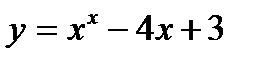 , осями координат и прямой х=4.
, осями координат и прямой х=4.
8.10 Найти площадь фигуры, заключенной между прямыми у=2х, у=5х, х=2, х=6.
8.11 Найти площадь части гиперболы 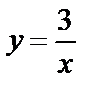 , отсекаемой от нее прямой х+у-4=0.
, отсекаемой от нее прямой х+у-4=0.
8.12 Найти площадь фигуры, отсекаемой от параболы 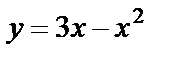 прямой 5х-у-8=0.
прямой 5х-у-8=0.
8.13 Вычислить площадь фигуры, ограниченной параболой 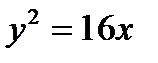 и прямой у=х.
и прямой у=х.
8.14 Найти площадь фигуры, заключенной между параболами 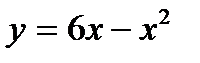 и
и 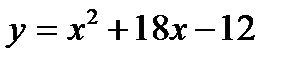 .
.
8.15 Вычислить площадь фигуры, заключенной между параболами 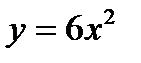 и
и 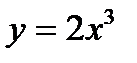 .
.
Задание 9.
Вычислить длину дуги.
9.1. y2 = x3 от х=0 до х=5
9.2. y=lnsinx от х= 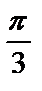 до х=
до х= 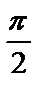
9.3. 2у= x2 -3 между точками пересечения с осью Ox
9.4. x= 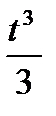 - t, y=t2+2 от t=1 до t=4
- t, y=t2+2 от t=1 до t=4
9.5. x=4(t-sint), y=4(1-cost) (длину дуги одной арки циклоиды)
9.6. 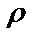 =5sin
=5sin 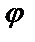
9.7. 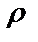 =sin3
=sin3 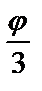 от
от 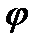 =0 до
=0 до 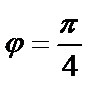
9.8. y=lnx от х= 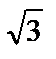 до x=2
до x=2 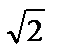
9.9. x= 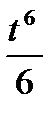 , y=2-
, y=2- 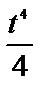 (между точками пересечения с координатными осями)
(между точками пересечения с координатными осями)
9.10. 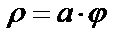 (длину первого витка спирали Архимеда)
(длину первого витка спирали Архимеда)
9.11. x= 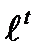 cost, y=
cost, y= 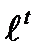 sint от t=0 до t=ln
sint от t=0 до t=ln 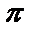
9.12. 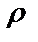 =1-cos
=1-cos 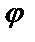
9.13. 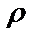 =2sin
=2sin 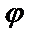
9.14. 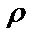 =2sin3
=2sin3 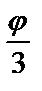
9.15. x 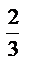 +y
+y 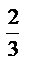 =9
=9
Задание 10.
10.1. Вычислить объём тела, образованного вращением вокруг оси фигуры, ограниченной дугой кубической параболы y=x3-4x и осью абсцисс.
10.2. Определить объём тела, полученного в результате вращения вокруг оси ОХ фигуры, которая ограничена дугой окружности х2+y2=16, лежащей в I четверти, и прямыми х=1 и х=3.
10.3. Найти объём тела, образованного вращением эллипса 4x2+9y2=36 вокруг малой оси.
10.4. Фигура, ограниченная дугой эллипса 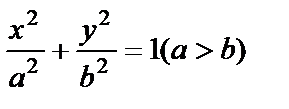 и двумя прямыми, перпендикулярными к оси абсцисс и проходящими через фокусы эллипса, вращается вокруг оси ОХ. Определить объём тела вращения.
и двумя прямыми, перпендикулярными к оси абсцисс и проходящими через фокусы эллипса, вращается вокруг оси ОХ. Определить объём тела вращения.
10.5. Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной ветвью гиперболы x2-y2=1 и прямой х=3.
10.6. Найти объем тела, образованного вращением астероиды x=acos3t, y=asin3t вокруг оси ОХ.
10.7. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной одной аркой циклоиды х=a(t-sint), y=a(1-cost) и отрезком 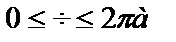 оси абсцисс.
оси абсцисс.
10.8. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами y=2x2 и y=x3.
10.9. Фигура, образованная в результате пересечения параболы y2=4x и прямой y=x, вращается вокруг оси Ох. Найти объём тела вращения.
10.10. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой y2=2x и прямой 2х+2у-3=0.
10.11. Вычислить объем тела, образованного вращением общей части парабол y=x2 и y2=8x: а)вокруг оси Ох; б)вокруг оси Оу.
10.12. Фигура, ограниченная кривыми y=tgx, y=ctgx и прямой x= 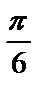 , вращается вокруг оси OX. Найти объем тела вращения.
, вращается вокруг оси OX. Найти объем тела вращения.
10.13. Найти объем тела, полученного в результате вращения вокруг оси OX сегмента, отсекаемого прямой х+у-2=0 от круга, граничная окружность которого x2+y2=4
10.14. Определить объем тела, образованного вращением вокруг оси ОY фигуры, ограниченной кривыми y=log2x, y=log4x и прямой y=1.
10.15. Фигура, лежащая в I четверти и ограниченная дугой окружности x2+y2=18, параболой 3y=x2 и осью ординат, вращается вокруг оси Ох. Найти объем тела вращения.
Задание 11.
11.1. Найти силу давления жидкости на вертикальную треугольную пластинку с основанием а и высотой h, погруженную в жидкость так, что вершина пластинки лежит на поверхности.
11.2. Скорость точки меняется по закону. Найти путь, пройденный точкой за первые девять секунд после начала движения.
11.3. Автомобиль, двигающийся со скоростью 48м/с., начинает тормозить и останавливается через 3с. Найти путь, пройденный автомобилем до полной остановки.
11.4. Реактивный самолет в течение 20с увеличил свою скорость от 360 до 720 м/с. Считая его движение равноускоренным, найти с каким ускорением летел самолет и какое расстояние пролетел он за это время.
11.5. С высоты 294м вертикально вниз брошено тело с начальной скоростью 19,6 M/с. Через сколько секунд тело упадет на землю? ( Ускорение силы тяжести принять равным 9,8м/с)
11.6. Найти работу, производимую при растяжении пружины на 5см, если известно, что сила, которая требуется для растяжения пружины, пропорциональна ее удлинении и что для удлинения пружины на I см требуется сила 1H.
11.7. Какую работу нужно затратить, чтобы выкачать воду из цилиндрического резервуара, радиус основания которого равен 3м, а высота равна 5m?
11.8. Найти работу, необходимую для выкачивания воды из конической воронки, обращенной вершиной вниз, если высота ее равна Н, а радиус основания r. Как изменится результат, если воронка будет обращена вершиной вверх?
11.9. Вычислить работу, которую надо затратить, чтобы выкачать воду из котла, имеющего форму полушара с радиусом, равным 1м.
11.10. Найти работу, необходимую для выкачивания воды из котла, имеющего форму полуцилиндра с радиусом основания r и высотой H.
11.11. Найти силу давления воды на прямоугольные ворота шлюза, ширина которых 25м, а глубина 18м, если их верхняя грань лежит на свободной поверхности воды. Определить также силу давления на нижнюю половину ворот шлюза.
11.12. Вычислить силу давления жидкости на вертикальный треугольный щит с
основанием а и высотой h, погруженный жидкость так, что основание щита лежит на её свободной поверхности.
11.13. Найти силу давления на плоскость полукруга с радиусом 6см, погруженного в воду вертикально, если его диаметр лежит на свободной поверхности воды.
11.14. Вертикальная пластина имеет форму трапеции, верхнее и нижнее основания которой соответственно равны 80см и 50см, а высота 20м. Вычислить силу давления на всю плотину.
11.15. Определить массу стержня длины 50см, если его линейная плотность меняется по закону 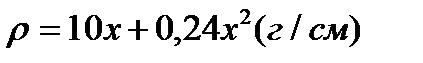 , где x – расстояние от одного из концов стержня.
, где x – расстояние от одного из концов стержня.
Задание 12.
Вычислить несобственный интеграл (исследовать его сходимость).
12.1. 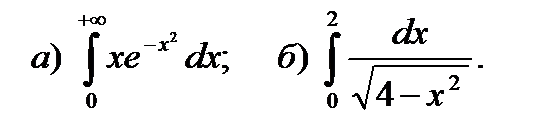
12.2. 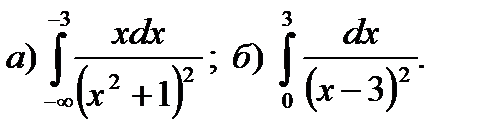
12.3. 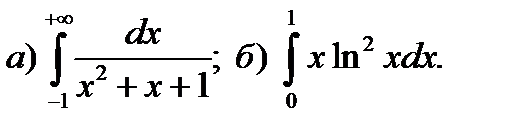
12.4. 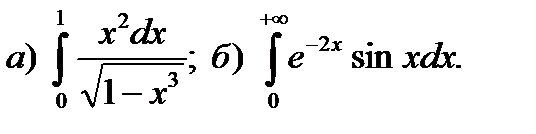
12.5. 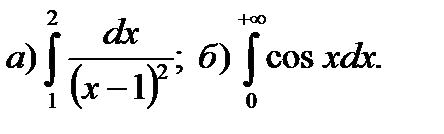
12.6. 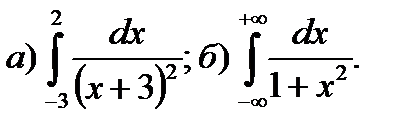
12.7. 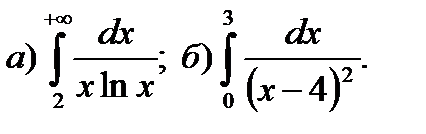
12.8. 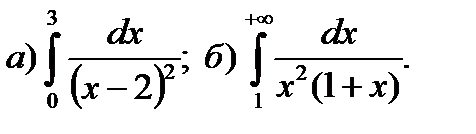
12.9. 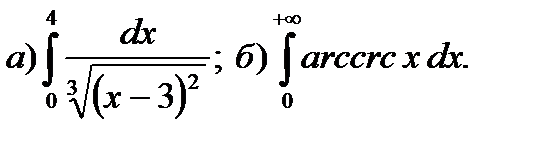
12.10. 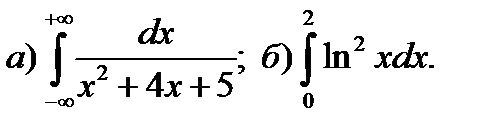
12.11. 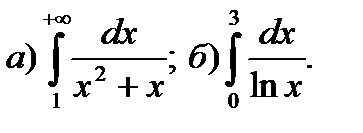
12.12. 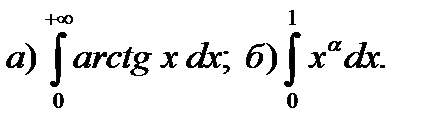
12.13. 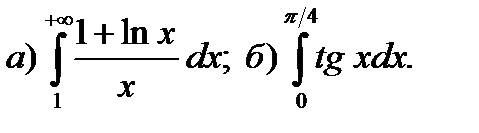
12.14. 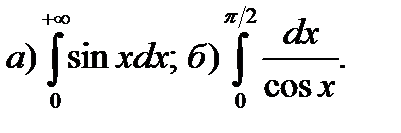
12.15. 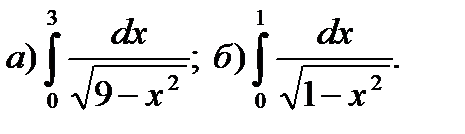
Дата добавления: 2016-06-05; просмотров: 3244;











