СКОРОСТЬ МАТЕРИАЛЬНОЙ ТОЧКИ

Предварительно сформулируем необходимые определения(см. рисунок 1.2):

Ø 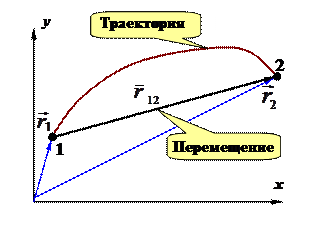Траекторией материальной точки будем называть воображаемую линию, вдоль которой движется частица. (Очевидно, что траектория – это, как и сама материальная точка, воображаемый объект, модель.)

Ø Путь,пройденный материальной точкой– скалярная величина, равная расстоянию, отсчитанному вдоль траектории при движении частицы из некоторой точки 1 в точку 2, .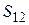

Ø

Рисунок 1.2.

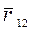Перемещениев результате движения из точки 1 в точку 2– вектор , проведенный из точки 1 в 2 траектории. Очевидно, что перемещение 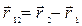. С другой стороны разность конечного и начального значения радиус-вектора есть его приращение: 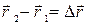. Поэтому можно считать, что можно считать, что перемещениепредставляет собойприращение радиус-вектора.

Движение частицы называется равномерным, если в любые равные промежутки времени частца проходит одинаковые пути (независимо от формы траектории!).

Важнейшим понятием кинематики является скорость материальной точки. На качественном уровне под скоростью в физике понимают векторнуювеличину, характеризующую быстроту перемеще-ния частицы по траектории и направление, в котором движется частица.

На бытовом уровне скорость можно найти, разделив путь, пройденный телом 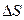за промежуток времени 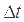, на величину этого промежутка. Такой расчет дает, очевидно, приближенное значение скорости, а о направлении скорости вообще ничего не позволяет сказать.

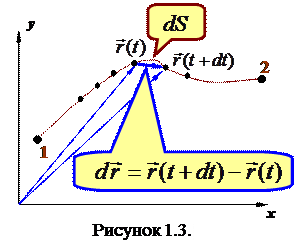Чтобы дать более строгое определение скорости поступим следующим образом: разобьем мысленно траекторию на участки 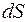, которые частица проходит за бесконечно малые промежутки времени 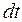(рисунок 1.3.). Каждому участку 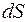соответствует перемещение 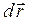за соответствующий 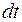. Для бесконечно малого 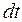можно утверждать, что модуль перемещения равен пути точки:

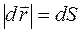, (1.4)

и траекторию можно считать состоящей из элементов 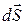, направленных в сторону перемещения частицы и совпадающих с 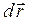. Можно считать, что за бесконечно малый 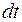движение тела не меняется. Отношение 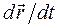дает векторную характеристику быстроты движения точки, модуль которой совпадает с традиционным представлением о скорости.

Поэтому по определению скоростью частицы называется производная ее радиус-вектора по времени:

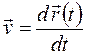(1.5)

Поскольку модуль приращения радиус-вектора за время 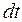совпадает по формуле (1.4) с элементом траектории 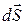, то в каждой точке траектории вектор скорости направлен по касательной к траектории в сторону движения частицы. Соответственно орт вектора скорости 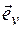совпадает с ортом касательной к траектории в данной точке, направленным в сторону движения частицы. Орт касательной к траектории принято обозначать 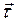. Поэтому для вектора скорости в данной точке траектории справедливо соотношение:

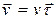(т.е. 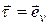) (1.6)

Учитывая, что выражение для радиус-вектора через его проекции на оси координат имеет вид 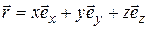, для вектора скорости можно записать представление через его проекции на оси координат :

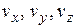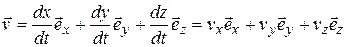, (1.7)

Как следует из соотношения (1.7), проекции вектора скорости на оси координат равны производным по времени проекций радиус-вектора, а составляющие вектора скорости по осям координат получаются умножением соответствующих производных на орты осей системы координат:

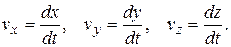(1.8)

(Напомним: проекции – это алгебраические скалярные величины, составляющие – это векторы, которые в сумме дают данный вектор).

В соответствии со своим определением вектор скорости характеризует быстроту изменения радус-вектора частицы. Радус-вектор 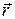может изменяться по модулю и по направлению. Следует предположить, что вектор скорости всегда можно представить в виде суммы двух векторов, один из которых характеризует изменение 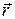только по модулю, а второй только по направлению. Действительно, как и любой вектор, 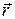можно представить в виде:

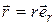. (1.9)

Находя производную по времени от этого выражения, получаем:

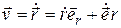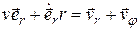= , (1.10)

Составляющая 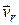направлена вдоль радиус вектора, а значит характерзует быстроту его изменения по мудулю. Направление второй составляющей, 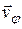, определяется производной орта радиус-вектора: 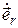. Как мы уже установили, производная орта определяется выражением (1.3)

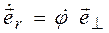. (1.11)

где 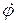– угловая скорость поворота радиус-вектора, а 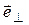- перпендикулярный к нему орт, направленный в сторону поворот㛇蚀㏝�夐ꃡ橞繹᤹뛱ඬᄿ␑帑⛿ṙ䀸칺㈚؏᩻�훵䒖砇ޥ꒨ু뛇㸁䯤飑ﾽ圌暁沦⻢�ﰶᨙ몯붚䫾Θ鴬쮣ࡥኋ既鳵৴㫂媩娒ᫍᆖ䨴ﻦ瞺㋼袭鍿賧妐짣䬗陾槰任ꑰ秸櫋䰤꜕䠏ﶪ�㉼䋂㿯괊锍㹊骈憳꿥㜘훅⦀⮸䪔퀲퍾㋹粚⵵Ꮚ充ꓲʷ难끧૜袋쑷鷐苼俅稇㸋㭖᚞᷋퍉ꤽ雵밂若꧴듗袙湄盳䕦섣㺘椧㏹㾗쮔鄨ꜛ䈁䊡借ｦ降黨噝㎚�贽㻖拕⤻婲᭳畜磡鉅麟퉜럳૳庑ᓦ଩誡熸䘑�둶ꝷ颯藨뀙嶚蜘俞⺪풓慅앦䈙呉쑢왞︕껈㍢伪ꅬ毥욀权ꁯ罌ꞯ蹱ゖ꠩┤硏⬂㏏䰼褩杰懪댸梼ዩ축鲒ꛋ໮刬㖎㫮寿뤱ם龌兦滣⚨霟氲넜醙찷⽌⦳І闆嘶䀡휮헧涶㟝ᄐΏ蓔㴢ㅇ⨇➫㮱튧�䏻၄ꑳⰼ흥嵂œ⼬껚专涃⩃⥫ݿ쮒㋣؆ྖ턘⤎ꓹ﮽켂㍳ⵡ蒂改귽蚫蓥鬺຾ꈀ炱퀰삼悺ᨏ贌핮灹맇床운걽㙥⤏썰疴蠟�틐ﯗࣉ⃄퀧ꇐณ폦휡섰㙩贷酞픂桳湉뵞遟᷏ꚥ夫댽㕜溬큻佊䵯用怅쎛钱皊9櫶₿䚛胷࣍鈬⇝늎볹ꏡ멅⩏鬽缶풅ⳮ菛크�Ј耵꺗�⿞᦬媎꿦픦猅늒䇰룎嗂㪷木掬住뀽♒꧱⨖翨鿔鈭궜数퀷ᬻ샤楐�橰㯹㱮ꪨ䶜﹁廲⩠쿥ͤ㙌씎ᐮ䔐錏爓뜯ꛒ䭊匥ᖢ欛ݒ䃧⒖ꙝꋘ羉ﬥ啯⃡㉈䠚먗㒮䀞촒Ố䌄즕牢焅财횸範ᅞ㲃聝❜턜잿悰ਭ】⒖兏ꤩ뽍頇匊盧ᨲ䘣欪絮삣ႀႪ쫑鐄䌡厛欧Ġ㜖ᔌ䈟饩㎚律磄ర�ᒅная пути по времени?! Чтобы ответить на этот вопрос необходимо вспомнить о том, что модуль приращения радиус-вектора совпадает с элементом траектории 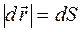. Тогда модуль соотношения, определяющего скорость,

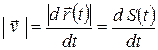. (1.13)

Таким образом, производная пути по времени дает модуль вектора скорости:

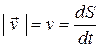, (1.14)

<1 234 5 6 7 >

Дата добавления: 2017-01-26; просмотров: 4180;

Поиск по сайту

Узнать еще