ВЕКТОРЫ И ДЕЙСТВИЯ С НИМИ
Многие физические величины (перемещение, скорость, сила, и т.д.) являются векторными, поэтому твердое знание основных сведений о векторах и действиях с нимиявляется совершенно необходимой предпосылкой успешного изучения курса общей физики. Перечислим основные сведения о векторах, необходимые для дальнейшего:
| 1. Определение вектора. 2. Модуль вектора. 3. Коллинеарные и компланарные векторы. 4. Сложение и вычитание векторов. 5. Умножение вектора на скаляр. 6. Единичный вектор (орт). 7. Проекция вектора на заданное направление. 8. Выражение вектора через его проекции на координатные оси. | 9. Компоненты вектора. 10. Радиус-вектор. 11. Скалярное произведение векторов. 12. Векторное произведение векторов. 13. Смешанное произведение векторов. 14. Двойное векторное произведение векторов. |
В качестве примера действий с векторами рассмотрим производную по времени единичного вектора 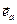 , задающего направление вектора
, задающего направление вектора 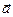 . Единичный вектор по определению имеет постоянный модуль, а значит изменяться может только по направлению.
. Единичный вектор по определению имеет постоянный модуль, а значит изменяться может только по направлению.
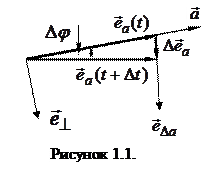 Допустим, что за очень малый промежуток времени
Допустим, что за очень малый промежуток времени 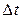 вектор
вектор 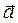 , а вместе с ним и орт
, а вместе с ним и орт 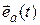 поворачивается на угол
поворачивается на угол 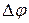 . В результате
. В результате 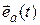 получает приращение
получает приращение 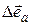 =
= 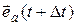
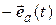 , направление которого задается ортом этого приращения
, направление которого задается ортом этого приращения 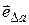 .
.
При малом 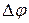 (и, соответственно,
(и, соответственно, 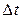 ) орт приращения вектора
) орт приращения вектора 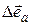 , т.е. вектор
, т.е. вектор 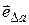 , можно считать практически перпендикулярным вектору
, можно считать практически перпендикулярным вектору 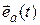 , а вектор
, а вектор 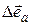 – катетом прямоугольного треугольника, противолежащим углу
– катетом прямоугольного треугольника, противолежащим углу 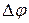 . Тогда модуль приращения орта
. Тогда модуль приращения орта 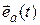 ,
,
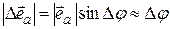 . (1.1)
. (1.1)
(Гипотенуза треугольника – вектор 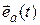 имеет единичную длину (ведь это единичный вектор!), а
имеет единичную длину (ведь это единичный вектор!), а 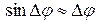 при малых
при малых 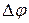 (– проверьте на калькуляторе, если угол выражать в радианах!).
(– проверьте на калькуляторе, если угол выражать в радианах!).
Таким образом, представив 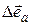 в виде произведения его модуля
в виде произведения его модуля 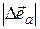 на орт приращения
на орт приращения 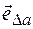 , можем записать (а так можно представить любой вектор!):
, можем записать (а так можно представить любой вектор!):
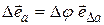 (1.2)
(1.2)
Необходимо учесть, что при 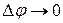 орт
орт 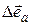 поворачивается и в пределе совпадает по направлению с ортом
поворачивается и в пределе совпадает по направлению с ортом 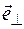 перпендикуляра к вектору
перпендикуляра к вектору 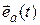 , направленным в сторону поворота
, направленным в сторону поворота 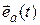 , как это показано на рисунке 1. (Вектор
, как это показано на рисунке 1. (Вектор 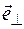 лежит в той плоскости, в которой поворачивается вектор
лежит в той плоскости, в которой поворачивается вектор 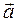 ). Тогда производная по времени орта
). Тогда производная по времени орта 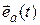 может быть представлена в виде:
может быть представлена в виде:
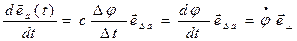 . (1.3)
. (1.3)
Забегая вперед, отметим, что по смыслу 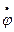 представляет собой угловую скорость вращения вектора
представляет собой угловую скорость вращения вектора 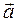 .
.
Дата добавления: 2017-01-26; просмотров: 1677;











