ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Классическая механика и границы ее применимости.

В основе классической механики лежат три закона Ньютона, сформулированные им в 1687 (!!!) году. Эти законы явились результатом обобщения большого количества экспериментальных фактов, и их справедливость подтверждается согласием следствий из них опытным данным для очень широкого, хотя и ограниченного, круга явлений.

Однако в начале ХХ века было установлено, что движение тел при скоростях, сравнимых со скоростью света в вакууме – с, подчиняется иным законам – законам релятивистской динамики. Релятивистская динамика основывается на специальной теории относительности Эйнштейна.При этом при малых скоростях законы релятивистской динамики практически совпадают с уравнениями классической механики в соответствии с принципом дополнительности в физике. Принцип дополнительности заключается в утверждении о том, что всякая новая теория в качестве некоего своего предельного случая включат в себя законы предыдущей теории.

Похожая ситуация сложилась при описании движения микрообъектов – частиц, сравнимых по массе с массой атома. Разработанная для описания таких объектов квантовая механика, для тел с большой массой дает такие же результаты, как классическая механика.

Таким образом, можно сказать, что классическая механика – это механика тел с массой намного больше масс атомов, движущихся со скоростями намного меньше скорости света в вакууме.

ЗАКОНЫ НЬЮТОНА

Первый закон утверждает: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения (говорят также, сохраняет состояние своего движения) до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Этот закон выполняется не во всех системах отсчета. Действительно: что если есть две системы отсчета, движущиеся друг относительно друга с ускорением, то первый закон не может одновременно выполняться в обеих системах отсчета.

Системы отсчета, в которых первый закон выполняется, называются инерциальными.

Экспериментально с очень высокой точностью установлено, что инерциальной является гелиоцентрическая система отсчета. (Гелиоцентрической называется система отсчета, начало координат которой расположено в центре солнца, а оси координат направлены на соответствующим образом выбранные звезды.) Можно доказать, что если некоторая система отсчета движется относительно инерциальной равномерно и прямолинейно, то она также является инерциальной.

Общеизвестно, что все тела препятствуют попыткам изменить состояние их движения, тело изменяет свою скорость движения только в том случае, если к нему приложена некоторая сила. Об этом свойстве тел говорят, что все тела обладают определенной инертностью. Количественной мерой инертности является массатела.

Если материальная точка с массой 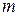движется со скоростью 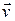, то по определению она обладает импульсом

(1.1)

Всякое протяженное тело можно представить в виде совокупности 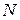материальных точек с массами 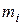, движущимися со скоростями 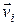. Импульсом такого тела называется величина

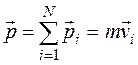(1.2)

Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на тело силе:

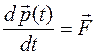(1.3)

Уравнение (1.3) называется уравнением движения тела.Учитывая важность этого уравнения, его часто называют такжеосновным уравнением динамики.

Известно, что в школьном курсе физике второй закон Ньютона формулируется несколько иначе – ускорение тела пропорционально приложенной силе и обратно пропорционально его массе:

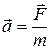. (1.4)

Возникает вопрос – какая из формулировок правильней? Обе справедливы! Но более общей является формулировка, выражаемая формулой (1.3). Действительно, подставим в уравнение (1.3) выражение для импульса (1.1):

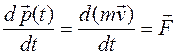(1.5)

В частном случае, когда масса тела считается постоянной, 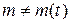,в уравнении (1.5) масса выходит из под знака производной и получаем:

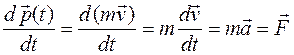, (1.6)

т.е. соотношение абсолютно эквивалентное формуле (1.4). Поэтому будем считать, что второму закону Ньютона соответствует уравнение (1.3). Правда в большинстве практических случаев масса тел может считаться постоянной, и с полным правом можно использовать традиционную формулировку – (1.4) или (1.6).

Третий закон Ньютона утверждает, что всякое действие одного тела на другое имеет характер взаимодействия и силы, с которыми действуют друг на друга взаимодействующие тела равны по величине и противоположны по направлению:

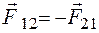, (1.7)

Как и большинство законов физики, этот закон имеет ограниченную область применения: третий закон всегда выполняется при контактных взаимодействиях тел, а также при взаимодействии на расстоянии покоящихся тел. Если взаимодействующие на расстоянии тела движутся друг относительно друга, то третий закон может нарушаться. Такое, в частности, возможно при взаимодействии заряженных тел.

<3 4 567 8 9 >

Дата добавления: 2017-01-26; просмотров: 1257;

Поиск по сайту

Узнать еще