Принцип относительности Галилея
 Рассмотрим две инерциальные системы отсчета и обозначим одну из них
Рассмотрим две инерциальные системы отсчета и обозначим одну из них 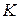 , а другую
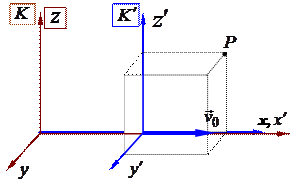
, а другую 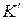 . Будем считать, что оси координат сориентированы так, как это показано на рисунке 1.2. (Отметим, что столь специальный выбор взаимной ориентации осей координат обеспечивает существенное упрощение сопутствующих математических выкладок, а результаты, которые мы будем обсуждать, имеют общий характер, т.е. справедливы при произвольной ориентации осей координат.) Будем считать систему
. Будем считать, что оси координат сориентированы так, как это показано на рисунке 1.2. (Отметим, что столь специальный выбор взаимной ориентации осей координат обеспечивает существенное упрощение сопутствующих математических выкладок, а результаты, которые мы будем обсуждать, имеют общий характер, т.е. справедливы при произвольной ориентации осей координат.) Будем считать систему 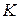 неподвижной, а систему
неподвижной, а систему 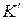 движущейся относительно
движущейся относительно 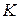 со скоростью
со скоростью 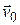 , направленной вдоль оси x (
, направленной вдоль оси x ( 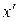 ).
).
Представим себе неподвижную в 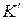 точку
точку 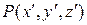 . Координаты этой точки системе отсчета
. Координаты этой точки системе отсчета 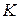 –
– 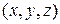 и время
и время 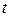 связаны с координатами и временем в
связаны с координатами и временем в 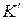 очевидными соотношениями:
очевидными соотношениями:
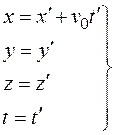 . (1.8)
. (1.8)
Система уравнений (1.8), уравнения которой связывают координаты точки в неподвижной и движущейся системах отсчета, называется преобразованиями Галилея.
Чтобы найти связь между компонентами векторов скоростей в 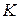 и
и 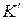 продифференцируем уравнения (1.8) по времени:
продифференцируем уравнения (1.8) по времени:
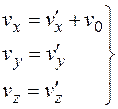 . (1.9)
. (1.9)
Соотношения (1.9) можно заменить одним векторным:
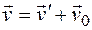 , (1.10)
, (1.10)
Которое выражает правило сложения скоростей в классической механике.
Дифференцируя (1.10) по времени, найдем связь между ускорениями в 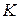 и
и 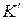 :
:
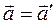 . (1.10)
. (1.10)
Соотношение (1.10) указывает на то, что ускорение тела во всех системах отсчета, движущихся равномерно и прямолинейно одинаково. Поэтому если одна из таких систем отсчета инерциальна, то и все другие также являются инерциальными.
Другой важный вывод, который следует из соотношения (1.10) заключается в следующем. Поскольку в основное уравнение динамики (1.6) из кинематических величин входит только ускорение, масса тел одинакова в различных системах отсчета, то и силы, действующие на тело в системах 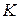 и
и 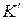 , должны быть одинаковы. Это означает, что уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой и все инерциальные системы отсчета эквивалентны.
, должны быть одинаковы. Это означает, что уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой и все инерциальные системы отсчета эквивалентны.
Иными словами это утверждение принято формулировать следующим образом: уравнения динамики инвариантны (т.е. неизменны) по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой(т.е. по отношению к преобразованиям Галилея). Это положение было установлено еще Галилеем и позволяет утверждать, что посредством проведения механических экспериментов невозможно определить, движется ли данная система отсчета равномерно и прямолинейно, или покоится. Если система отсчета неинециальна, движется неравномерно, с ускорением, то это легко обнаруживается экспериментально (Придумайте такой эксперимент!). А вот, например, равномерное и прямолинейное движение теплохода обнаружить механическими экспериментами невозможно.
Утверждение о том, чтоникакими механическими опытами невозможно установить движется ли данная инерциальная система отсчета равномерно и прямолинейно или покоится, называется ПРИНЦИПОМ ОТНОСИТЕЛЬНОС-ТИ ГАЛИЛЕЯ.
Дата добавления: 2017-01-26; просмотров: 1382;











