Кривые второго порядка.
Кривые эллипса, гиперболы и параболы, которые получаются при пересечении кругового конуса плоскостями, не проходящими через его вершину, называются кривыми второго порядка. Ниже дадим определения этих кривых, как геометрических мест точек на плоскости, и приведем их канонические уравнения.
Каноническое уравнение эллипса.
Эллипс – геометрическое место точек на плоскости, сумма расстояний которых от двух фиксированных точек (фокусов), есть величина постоянная (рис. 2.30).
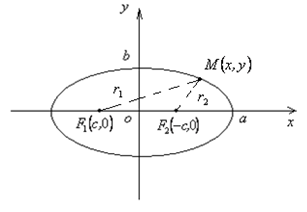
Рис. 2.30
Итак, имеем
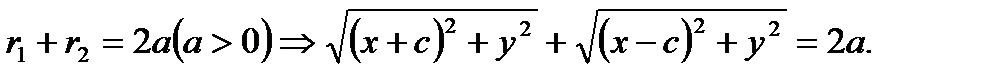 (2.73)
(2.73)
Рационализируя это уравнение, получим каноническое уравнение эллипса в виде
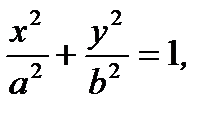 (2.74)
(2.74)
где 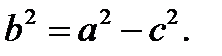 Величины
Величины 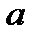 и
и 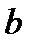 называются полуосями эллипса, а
называются полуосями эллипса, а 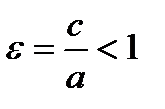 называется
называется
эксцентритетом эллипса. Заметим, что в случае 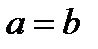 из (2.74) получим уравнение окружности, центр которой совпадает с началом координат. Она имеет вид
из (2.74) получим уравнение окружности, центр которой совпадает с началом координат. Она имеет вид
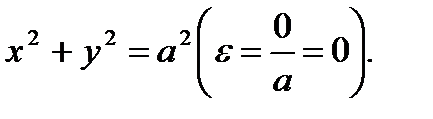
Пример 2.25.Составить уравнение эллипса, если известно, что его фокусы расположены на оси 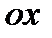 и
и 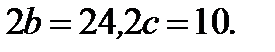
Решение.Из условий задачи имеем
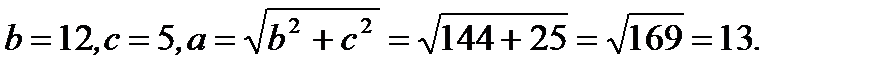
Тогда уравнение эллипса будет иметь вид 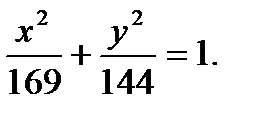
Ответ: 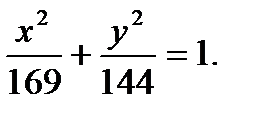
Дата добавления: 2021-05-28; просмотров: 527;











