Уравнения некоторых кривых в полярных координатах.
Положение точки на плоскости можно определить не только заданием ее прямоугольных координат 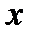 и
и 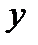 , а еще заданием, так называемых, полярных координат
, а еще заданием, так называемых, полярных координат 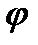 и
и 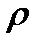 (рис. 2.24).
(рис. 2.24).
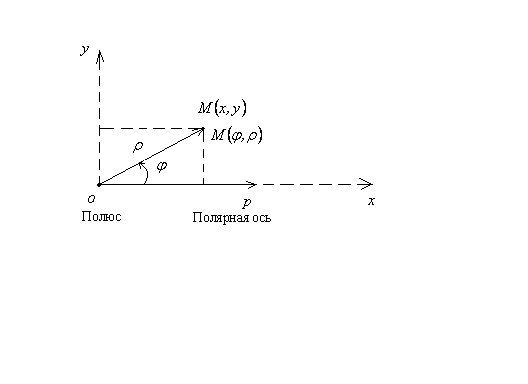
Рис. 2.24
Полярная система координат на плоскости определяется полюсом (точка  ) и полярной осью
) и полярной осью 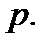
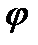 есть угол между полярной осью и вектором
есть угол между полярной осью и вектором 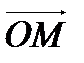 , а
, а 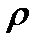 есть модуль вектора
есть модуль вектора 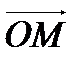 . Очевидно, что
. Очевидно, что
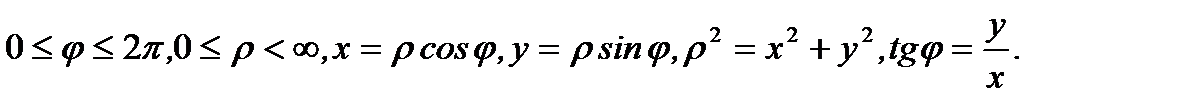
Пример 2.20.Окружность.
Если в уравнении окружности  вместо
вместо 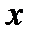 и
и 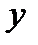 подставить
подставить 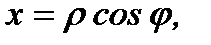
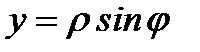 , то получим уравнение этой окружности в полярной системе координат в виде:
, то получим уравнение этой окружности в полярной системе координат в виде: 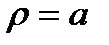 . График приведен на рисунке 2. 25.
. График приведен на рисунке 2. 25.
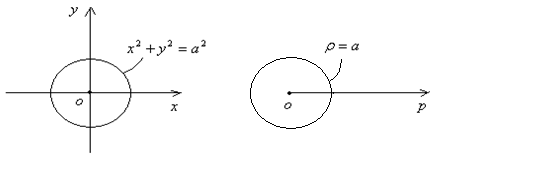
Рис. 2. 25
На самом деле, имеем
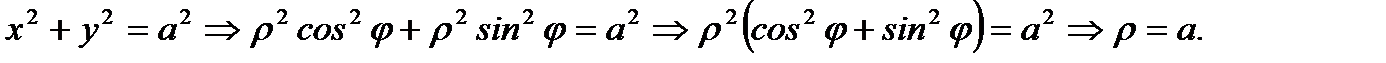
Пример 2.21.Лемниската Бернулли.
Если в уравнении лемнискаты 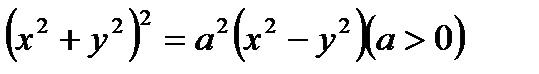 перейти к полярным координатам, то получим
перейти к полярным координатам, то получим
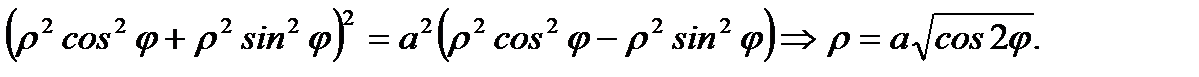
Итак, уравнение лемнискаты Бернулли в полярных координатах имеет вид: 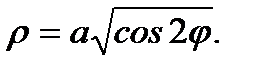
График приведен на рисунке 2. 26.
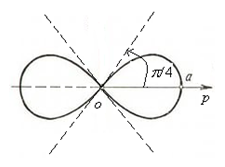
Рис. 2. 26
Пример 2.22.Спираль Архимеда.
Уравнение этой кривой в полярных координатах выражается формулой 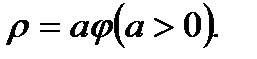 График приведен на рисунке 2. 27.
График приведен на рисунке 2. 27.
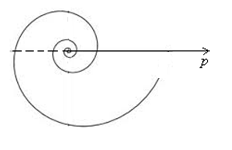
Рис. 2.27
Пример 2.23.Трехлепестковая роза.
Уравнение этой кривой в полярных координатах выражается формулой 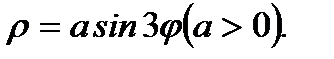 График приведен на рисунке 2. 28.
График приведен на рисунке 2. 28.
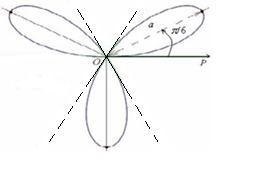
Рис. 2.28
Пример 2.24.Четырехлепестковая роза.
Уравнение этой кривой в полярных координатах выражается формулой 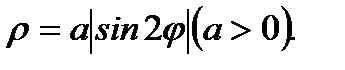 График приведен на рисунке 2. 29.
График приведен на рисунке 2. 29.
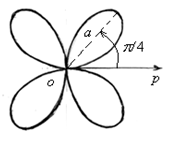
Рис. 2.29
Дата добавления: 2021-05-28; просмотров: 598;











