Различные виды уравнений прямой в пространстве.
1. Общие уравнения прямой в пространстве.
Прямую 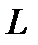 в пространстве можно рассматривать как линию пересечения двух плоскостей
в пространстве можно рассматривать как линию пересечения двух плоскостей 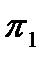 и
и 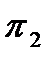 (рис. 2.23). То есть, общие уравнения прямой в пространстве можно представить в виде
(рис. 2.23). То есть, общие уравнения прямой в пространстве можно представить в виде
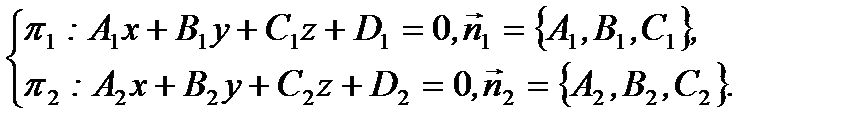 (2.67)
(2.67)
При решении многих задач удобно пользоваться так называемыми каноническими уравнениями прямой в пространстве. В эти уравнения входят такие величины, как координаты направляющего вектора 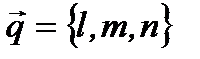 (параллельный вектор прямой в пространстве) и координаты точки
(параллельный вектор прямой в пространстве) и координаты точки 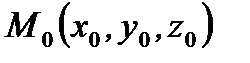 , принадлежащей прямой
, принадлежащей прямой 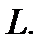 Если на прямой
Если на прямой 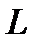 взять точку с текущими координатами (точка
взять точку с текущими координатами (точка 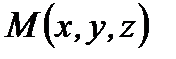 , то очевидно, что векторы
, то очевидно, что векторы 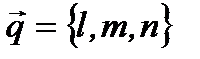 и
и 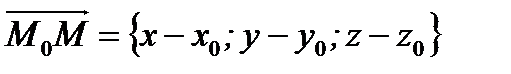 (рис. 2.23) коллинеарны, то есть (см. § 2.2)
(рис. 2.23) коллинеарны, то есть (см. § 2.2)
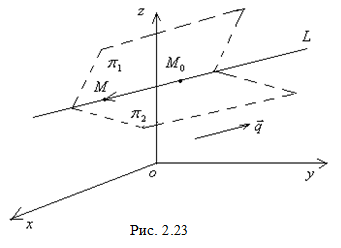
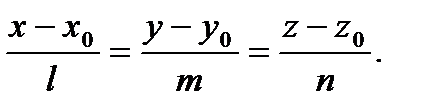 (2.68)
(2.68)
(2.68) и есть канонические уравнения прямой 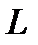 в пространстве. Заметим, что, например, если
в пространстве. Заметим, что, например, если 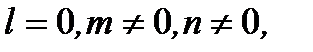 то имеем
то имеем
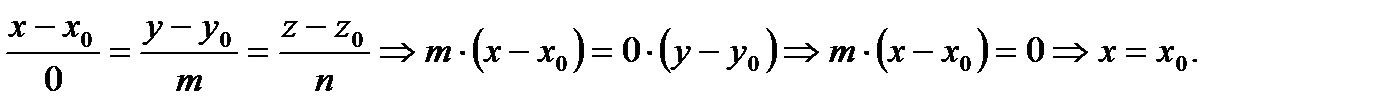
Метод приведения общих уравнений прямой в пространстве к каноническому виду покажем на примере экономического характера.
Пример 2.18.Предприятие выпускает трех видов продукции в количестве 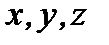 единиц. При применении первой технологии эти продукции приносят соответственно прибыль 20, 50, 30 руб. с единицы. При применении второй технологии эти продукции приносят соответственно прибыль 15, 40, 60 руб. с единицы. Определить производственные программы предприятия, дающие при разных технологиях одинаковую прибыль, равную 300 руб.
единиц. При применении первой технологии эти продукции приносят соответственно прибыль 20, 50, 30 руб. с единицы. При применении второй технологии эти продукции приносят соответственно прибыль 15, 40, 60 руб. с единицы. Определить производственные программы предприятия, дающие при разных технологиях одинаковую прибыль, равную 300 руб.
Решение.Из условий задачи имеем
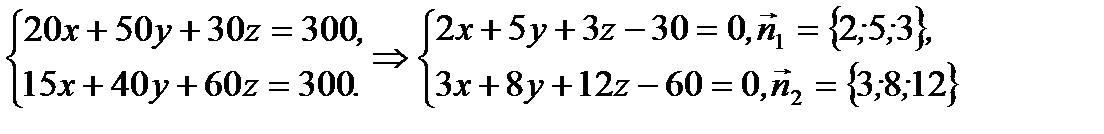 (2.69)
(2.69)
Как видно из (2.69), задача экономического характера математически сводится к общим уравнениям прямой в пространстве. Приведем эти уравнения к каноническому виду. Так как 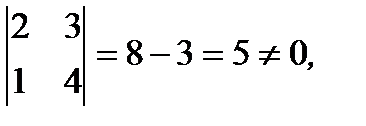 то
то 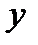 можно дать произвольное значение, например,
можно дать произвольное значение, например, 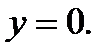 Тогда из (2.69) получим
Тогда из (2.69) получим
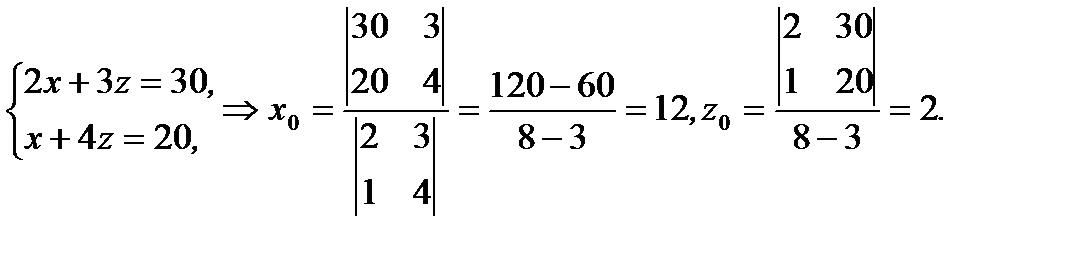
То есть нашли точку 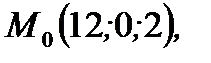 которая принадлежит прямой в пространстве. Далее заметим, что направляющий вектор
которая принадлежит прямой в пространстве. Далее заметим, что направляющий вектор 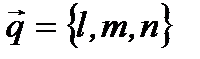 равен
равен
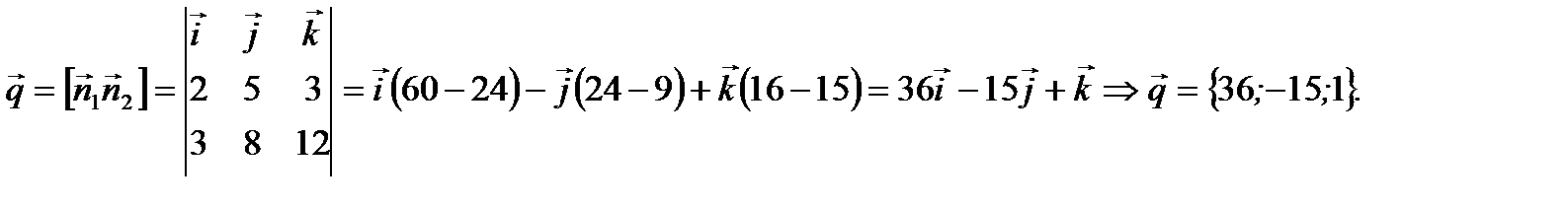
Тогда согласно (2.68) получим
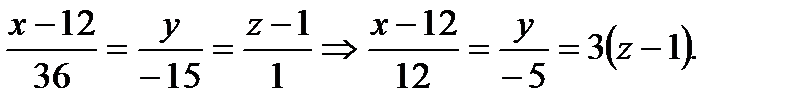
Ответ: 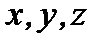 должны удовлетворять уравнениям
должны удовлетворять уравнениям 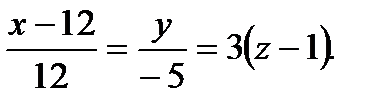
Отметим, что из канонических уравнений прямой в пространстве (2.68) можно получить параметрические уравнения прямой в пространстве. Для этого в канонические уравнения включим параметр 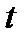 следующим образом
следующим образом
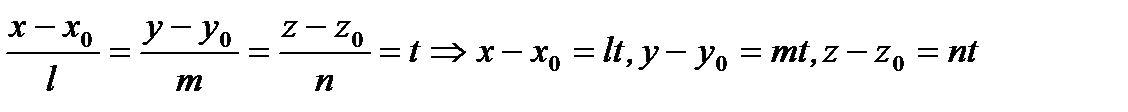
или
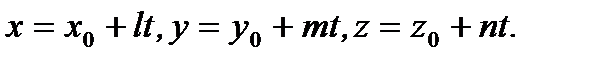 (2.70)
(2.70)
Уравнения (2.70) называются параметрическими уравнениями прямой в пространстве.
Пример 2.19.Составить уравнение плоскости 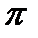 , проходящей через точку
, проходящей через точку 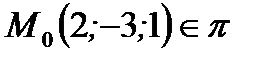 и через прямую
и через прямую 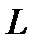 :
: 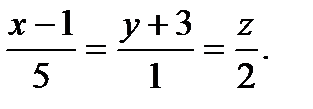
Решение.Пусть уравнение искомой плоскости 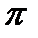 имеет вид
имеет вид
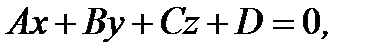 (2.71)
(2.71)
где 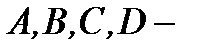 пока неизвестные числа. Основываясь на условия задачи, для неизвестных
пока неизвестные числа. Основываясь на условия задачи, для неизвестных 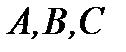 выраженные через
выраженные через 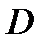 получим следующие три уравнения.
получим следующие три уравнения.
1. Плоскость 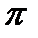 проходит через точку
проходит через точку 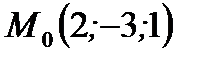 . То есть имеет место уравнение
. То есть имеет место уравнение
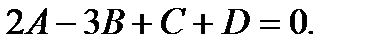
2. 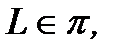 то есть
то есть 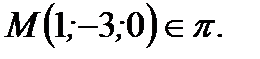 Последнее означает, что имеем уравнение
Последнее означает, что имеем уравнение
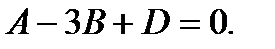
3. 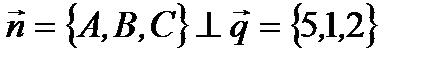 , то есть
, то есть 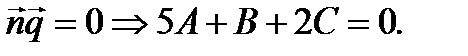
Итак, получили следующие три линейных уравнения относительно неизвестных 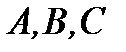
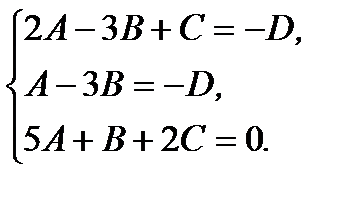
Решая систему по правилам Крамера, получим:
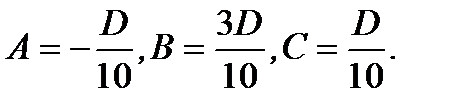 (2.72)
(2.72)
Подставляя (2.72) в (2.71) и поделив обе части уравнения на 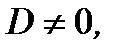 получим
получим
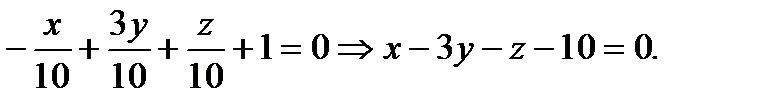
Ответ: 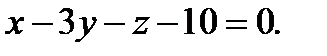
Дата добавления: 2021-05-28; просмотров: 528;











