Смешанное произведение трех векторов.
Смешанным произведением трех векторов 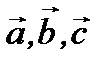 называется число, которое получается, когда два вектора (например,
называется число, которое получается, когда два вектора (например, 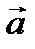 и
и 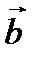 ) умножаются векторно и результат (вектор
) умножаются векторно и результат (вектор 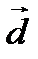 ) умножается на третий вектор
) умножается на третий вектор 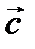 скалярно, то есть
скалярно, то есть 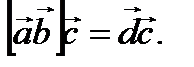 Отметим, что значение смешанного произведения не меняется при циклической перестановке векторов
Отметим, что значение смешанного произведения не меняется при циклической перестановке векторов
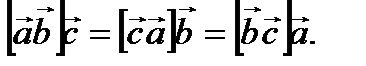
Геометрически модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах, как на сторонах (рис. 2.11), то есть
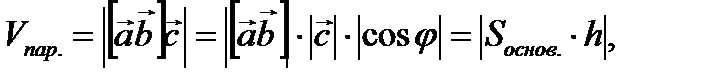 (2.24)
(2.24)
где 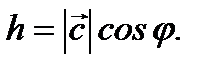 При этом если
При этом если 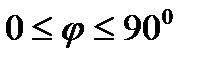 , то
, то 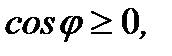 а если
а если 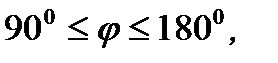 то
то 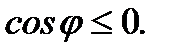

Если векторы даны своими координатами 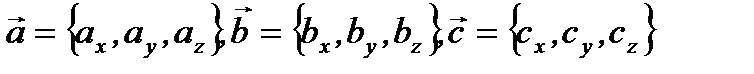 , то смешанное произведение этих векторов примет вид
, то смешанное произведение этих векторов примет вид 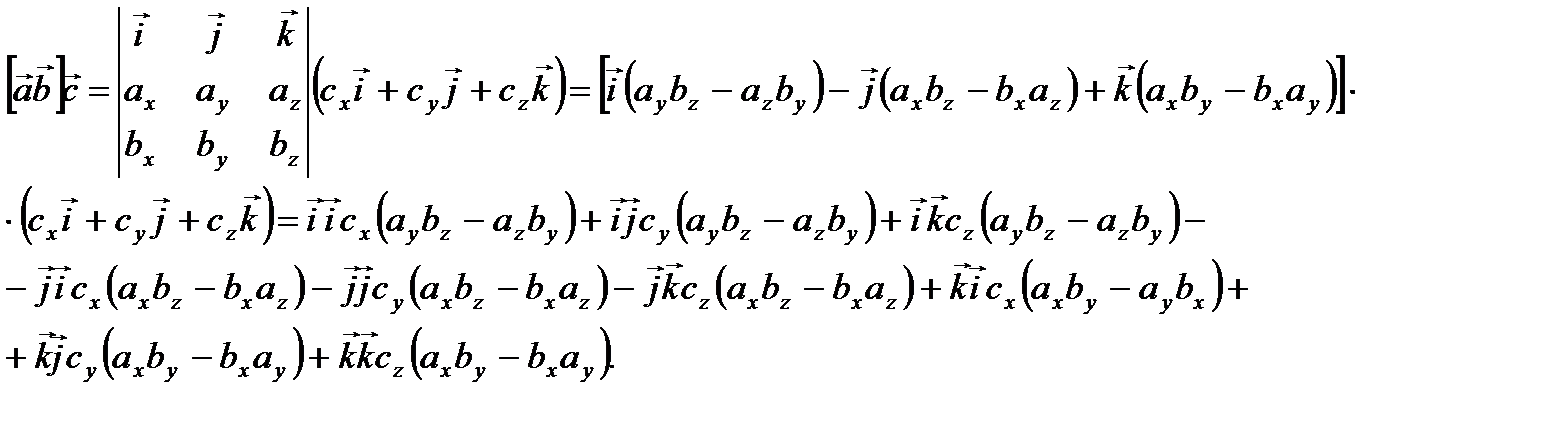 (2.25)
(2.25)
Учитывая, что 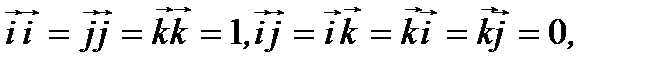 из (2.25) получим
из (2.25) получим
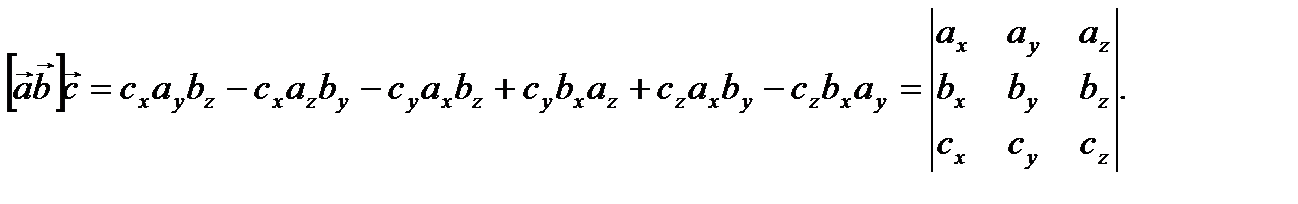 (2.26)
(2.26)
(2.16) представляет выражение смешанного произведения трех векторов в координатах.
Три ненулевых вектора 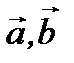 и
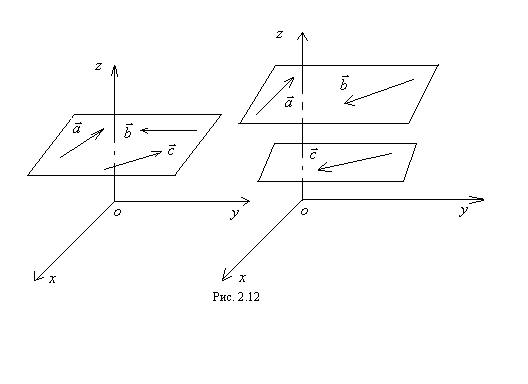
и 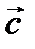 в трехмерной прямоугольной системе координат называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях (рис. 2.12).
в трехмерной прямоугольной системе координат называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях (рис. 2.12).
Теорема 2.3.Равенство нулю смешанного произведения трех ненулевых векторов 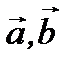 и
и 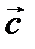
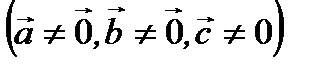 является необходимым и достаточным условием компланарности трех векторов.
является необходимым и достаточным условием компланарности трех векторов.
Доказательство:
Необходимость. Дано, что векторы 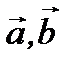 и
и 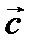 компланарны. Доказать, что
компланарны. Доказать, что 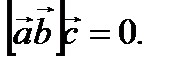
Так как по условию теоремы векторы компланарны, то векторное произведение 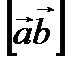
есть вектор, который перпендикулярен вектору 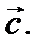 Но тогда их скалярное произведение равно нулю. Другими словами, на трех компланарных векторах, как на сторонах, нельзя построить параллелепипед.
Но тогда их скалярное произведение равно нулю. Другими словами, на трех компланарных векторах, как на сторонах, нельзя построить параллелепипед.
Достаточность. Дано, что 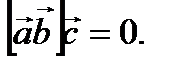 Доказать, что векторы
Доказать, что векторы 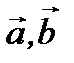 и
и 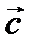 компланарны.
компланарны.
По условию теоремы векторное произведение 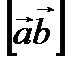 и вектор
и вектор 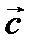 перпендикулярны. То есть, векторы
перпендикулярны. То есть, векторы 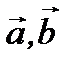 и
и 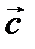 компланарны.
компланарны.
Пример 2.10. Показать, что векторы 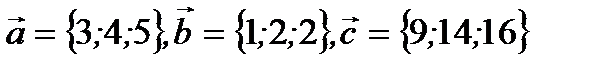 компланарны.
компланарны.
Решение.Вычислим 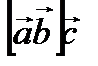 по формуле (2.16). Имеем
по формуле (2.16). Имеем
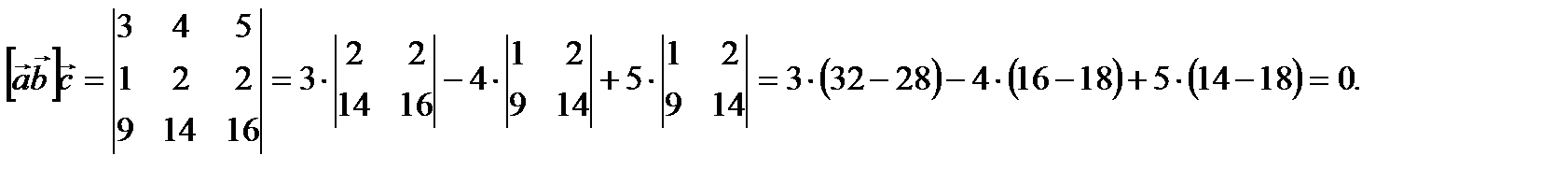 Тогда согласно теореме 2.3 векторы
Тогда согласно теореме 2.3 векторы 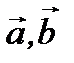 и
и 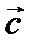 компланарны.
компланарны.
Ответ:векторы 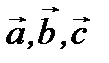 компланарны.
компланарны.
Дата добавления: 2021-05-28; просмотров: 613;











