Сумма и разность векторов. Представление вектора в координатах.
Если два вектора 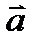 и
и 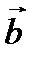 исходят из одного начала, то сумма этих векторов
исходят из одного начала, то сумма этих векторов 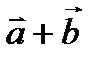 есть вектор, который получается, когда вектор
есть вектор, который получается, когда вектор 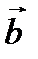 параллельно себя переносим так, чтобы его начало совпало с концом вектора
параллельно себя переносим так, чтобы его начало совпало с концом вектора 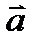 и соединяем начало вектора
и соединяем начало вектора 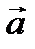 с концом вектора
с концом вектора 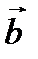 после параллельного переноса (рис. 2.5).
после параллельного переноса (рис. 2.5).
Если два вектора 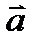 и
и 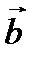 исходят из одного начала, то разность этих векторов
исходят из одного начала, то разность этих векторов 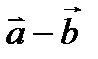 есть вектор, исходящий с конца вектора
есть вектор, исходящий с конца вектора 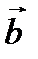 к концу вектора
к концу вектора 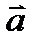 (рис. 2.5).
(рис. 2.5).
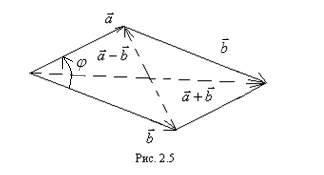
Отметим, что, как видно из рисунка 2.5, сумма векторов 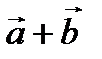 по модулю равна длине большей диагонали, а разность векторов
по модулю равна длине большей диагонали, а разность векторов 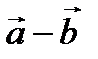 по модулю равна длине меньшей диагонали параллелограмма, построенного на этих векторах
по модулю равна длине меньшей диагонали параллелограмма, построенного на этих векторах 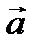 и
и 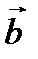 , как на сторонах.
, как на сторонах.
Пример 2.3. Найти 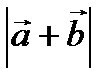 и
и 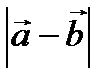 , если известно, что
, если известно, что 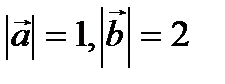 и угол между ними
и угол между ними 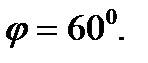
Решение.По теореме косинусов имеем
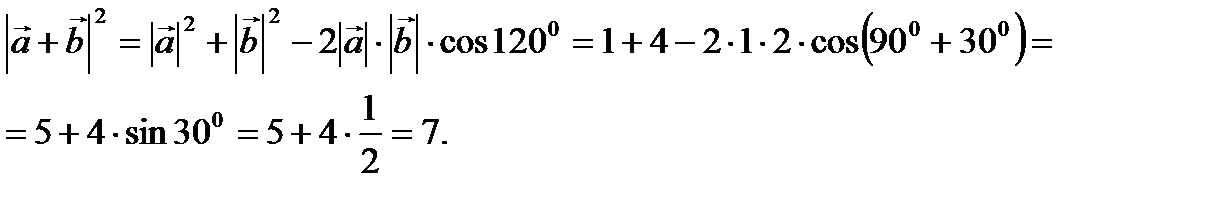
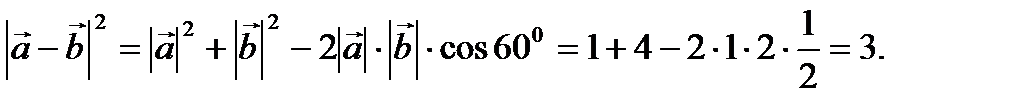
Тогда
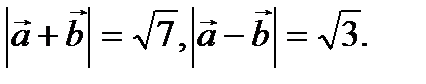
Ответ:
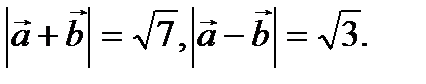
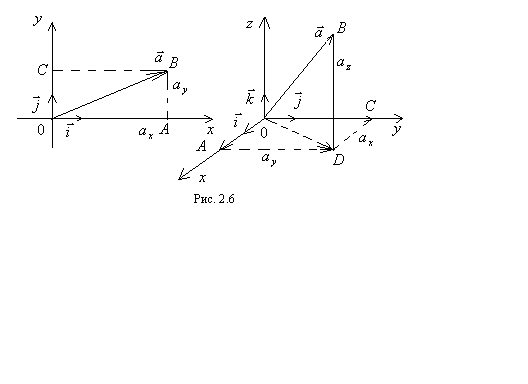
Вектор в двумерной и трехмерной прямоугольной системе координат можно представить в виде разложения по его координатам. Как известно, единичными векторами осей  и
и  в двумерной системе координат являются векторы
в двумерной системе координат являются векторы  и
и 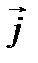 , a единичными векторами осей
, a единичными векторами осей 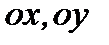 и
и 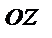 в трехмерной системе координат являются векторы
в трехмерной системе координат являются векторы 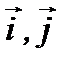 и
и 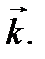 Модули единичных векторов равны единице
Модули единичных векторов равны единице 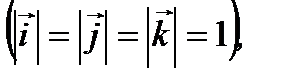 а их направления совпадают с положительными направлениями осей
а их направления совпадают с положительными направлениями осей 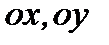 и
и 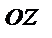 , соответственно. Эти единичные векторы составляют базис в прямоугольной системе координат. Рассмотрим вектор
, соответственно. Эти единичные векторы составляют базис в прямоугольной системе координат. Рассмотрим вектор 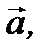 исходящий из начала координат (рис. 2.6). С конца вектора
исходящий из начала координат (рис. 2.6). С конца вектора 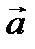 (точка
(точка 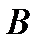 ) проведем перпендикуляры к осям
) проведем перпендикуляры к осям 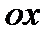 и
и 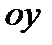 . Направленный отрезок
. Направленный отрезок 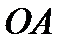 называется иксовой координатой вектора
называется иксовой координатой вектора 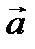 и обозначается через
и обозначается через 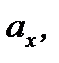 а направленный отрезок
а направленный отрезок 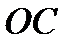 называется игрековой координатой вектора
называется игрековой координатой вектора 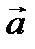 и обозначается через
и обозначается через 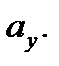 Очевидно, что
Очевидно, что 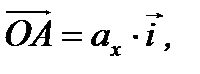 а
а 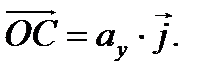 Но по правилам суммы векторов имеем
Но по правилам суммы векторов имеем 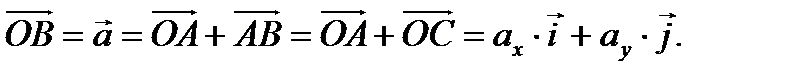 Итак, если
Итак, если 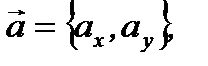 то разложение вектора
то разложение вектора 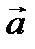 по его координатам имеет вид (рис. 2.6)
по его координатам имеет вид (рис. 2.6)
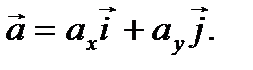 (2.11)
(2.11)
Аналогично, в трехмерной прямоугольной системе координат имеет место разложение вектора 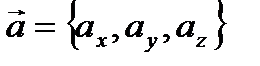 по его координатам
по его координатам 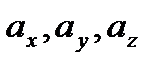 в виде (рис. 2.6)
в виде (рис. 2.6)
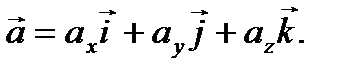 (2.12)
(2.12)
Отметим также, что на основе теоремы Пифагора можно модуль вектора выразить через его координаты следующим образом
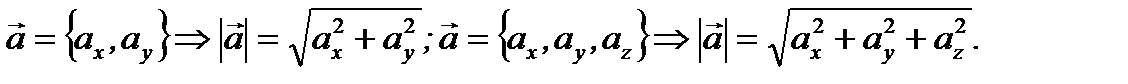
Пример 2.4. Дан вектор 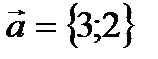 . Разложить его по базису
. Разложить его по базису 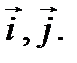
Решение.Согласно (2.11) имеем 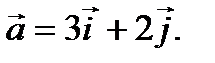
Ответ: 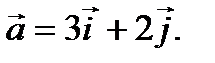
Дата добавления: 2021-05-28; просмотров: 752;











