Несобственный интеграл второго рода и его вычисление.
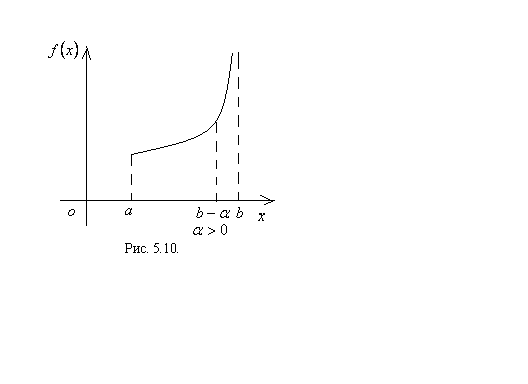
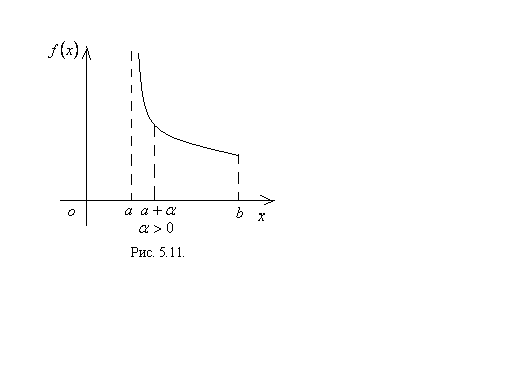
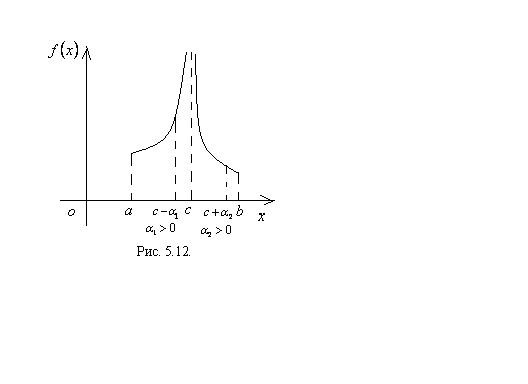
Если пределы интегрирования конечные числа, а подынтегральная функция в области изменения 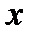 терпит разрыв второго рода (бесконечный разрыв), то имеем дело с несобственным интегралом второго рода (см. рисунки 5.10, 5.11, 5.12). Способ вычисления несобственного интеграла второго рода приведен ниже.
терпит разрыв второго рода (бесконечный разрыв), то имеем дело с несобственным интегралом второго рода (см. рисунки 5.10, 5.11, 5.12). Способ вычисления несобственного интеграла второго рода приведен ниже.
1. 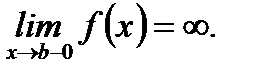
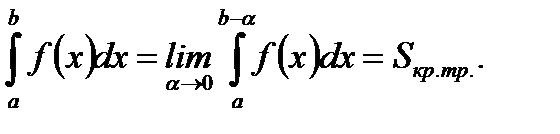 (5.60)
(5.60)
2. 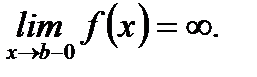
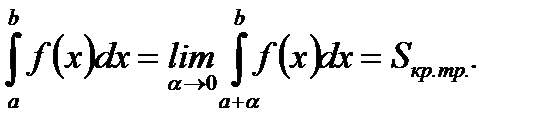 (5.61)
(5.61)
| ( |
| ) |
| ( |
| ) |
| ( |
| ) |
| . |
| S |
| dx |
| x |
| f |
| dx |
| x |
| f |
| lim |
| dx |
| x |
| f |
| . |
| тр |
| . |
| кр |
| c |
| a |
| b |
| c |
| b |
| a |
| = |
| ÷ |
| ÷ |
| ø |
| ö |
| ç |
| ç |
| è |
| æ |
| + |
| = |
| ò |
| ò |
| ò |
| - |
| + |
| ® |
| ® |
| a |
| a |
| a |
| a |
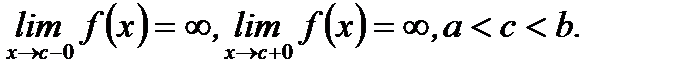
(5.62)
Если несобственный интеграл второго рода после вычисления равен конечному числу, то он сходится, то есть 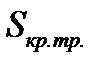 имеет конечное значение, а если
имеет конечное значение, а если  или вообще не определяется, то он расходится. Сходимость или расходимость несобственного интеграла зависит от правила или закона стремления к бесконечности при приближении к точке разрыва второго рода.
или вообще не определяется, то он расходится. Сходимость или расходимость несобственного интеграла зависит от правила или закона стремления к бесконечности при приближении к точке разрыва второго рода.
Выясним поведение несобственного интеграла второго рода от функции 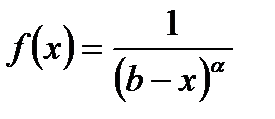 при различных значениях
при различных значениях 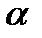 (см. рис. 5.10)).
(см. рис. 5.10)).
1. 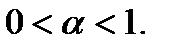
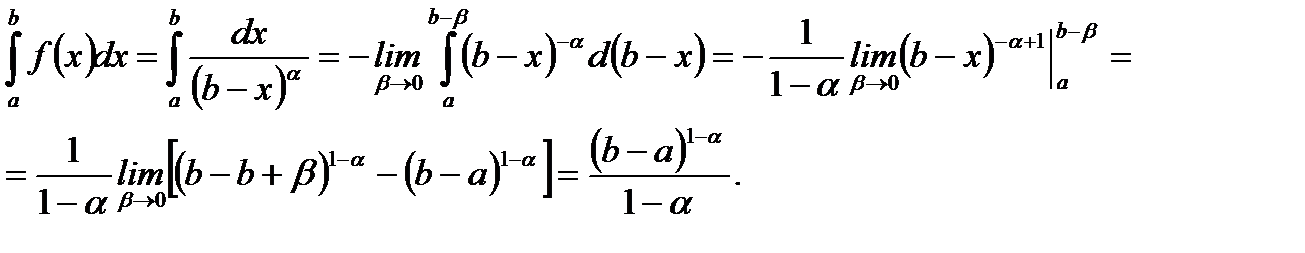 (5.63)
(5.63)
(5.63) показывает, что несобственный интеграл второго рода имеет конечное значение, то есть он сходится и 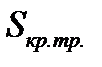 равна конечному числу.
равна конечному числу.
2. 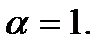
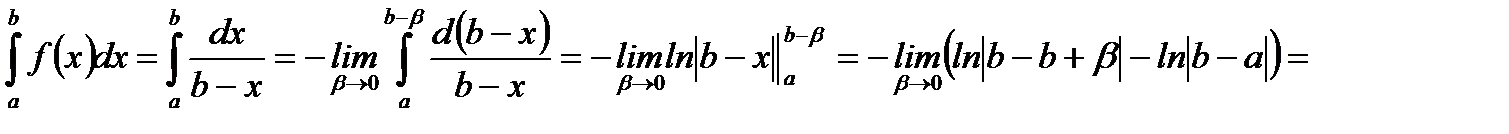
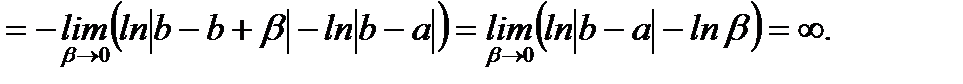 (5.64)
(5.64)
Как следует из (5.64) несобственный интеграл второго рода имеет конечное значение, то есть он сходится и 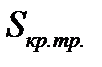 равна конечному числу.
равна конечному числу.
3. 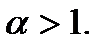
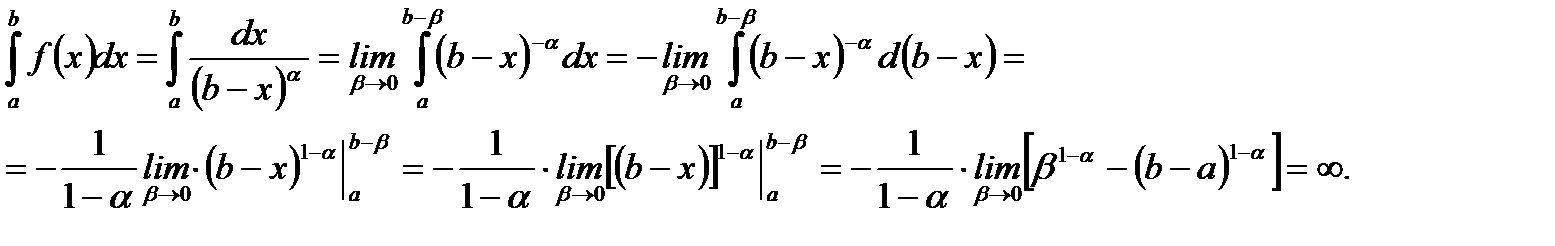 (5.65)
(5.65)
Согласно (5.65) несобственный интеграл второго рода расходится, то есть 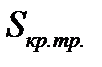 бесконечно большое число.
бесконечно большое число.
Пример 5.53.Вычислить интеграл
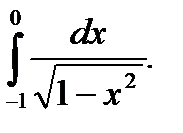
Решение.Заметим, что при 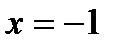 подынтегральная функция имеет разрыв второго рода.
подынтегральная функция имеет разрыв второго рода.
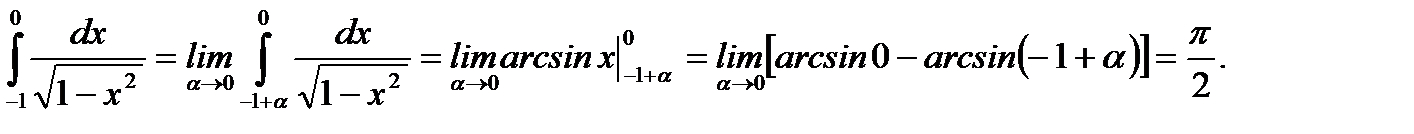
Ответ:интеграл сходится и 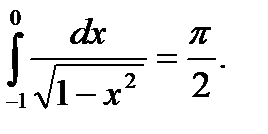
Задачи с ответами.
5.4.1. Вычислить неопределенный интеграл
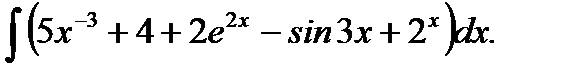
Ответ: 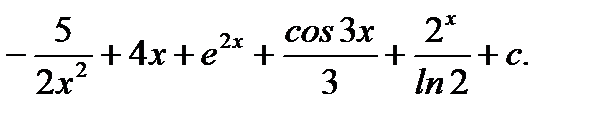
5.4.2. Вычислить неопределенный интеграл
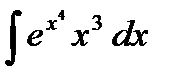 .
.
Ответ: 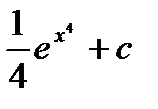 .
.
5.4.3. Вычислить неопределенный интеграл
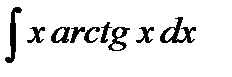 .
.
Ответ: 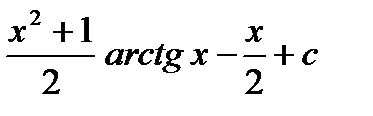 .
.
5.4.4. Вычислить неопределенный интеграл
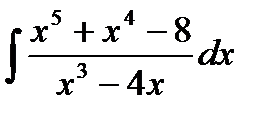 .
.
Ответ: 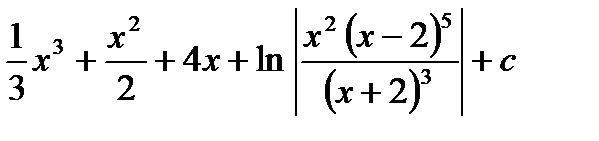 .
.
5.4.5. Вычислить определенный интеграл
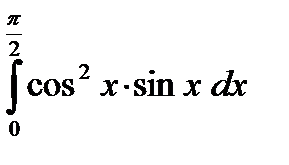
Ответ: 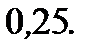
5.4.6. Вычислить определенный интеграл
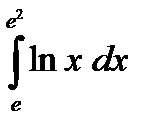
Ответ: 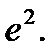
5.4.7. Вычислить площадь фигуры, ограниченной параболой
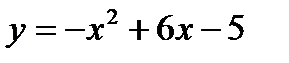 и осями координат.
и осями координат.
Ответ: 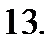
5.4.8. Вычислить длину дуги кривой 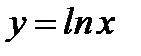 (от
(от 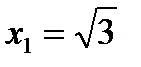 до
до 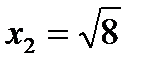 ).
).
Ответ: 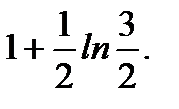
5.4.9. Вычислить площадь фигуры, ограниченной двухлепестковой розой 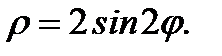
Ответ: 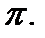
5.4.10. Вычислить несобственный интеграл первого рода 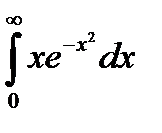 .
.
Ответ: 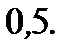

5.4.11. Вычислить несобственный интеграл первого рода 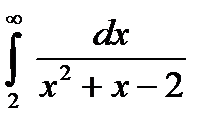 .
.
Ответ: 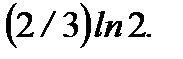
5.4.12. Вычислить несобственный интеграл первого рода 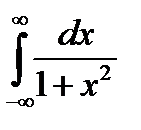 .
.
Ответ: 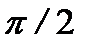 .
.
5.4.13. Вычислить несобственный интеграл второго рода 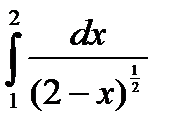 .
.
Ответ: 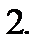
5.4.14. Вычислить несобственный интеграл второго рода 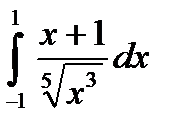 .
.
Ответ: 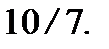
5.4.15. Вычислить несобственный интеграл первого рода 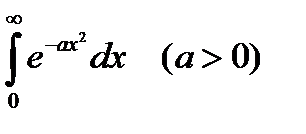 , пользуясь интегралом Пуассона
, пользуясь интегралом Пуассона 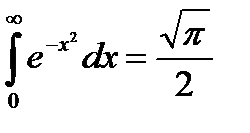 .
.
Ответ: 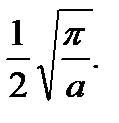

Дата добавления: 2021-05-28; просмотров: 486;











