Метод Лагранжа интегрирования дробно-рациональных функций.

Если под интегралом стоит частное двух многочленов относительно 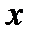одинаковой или различной степени, то имеем дело с интегрированием дробно-рациональной функции. При этом дробно-рациональные функции могут быть правильными и неправильными. Ниже приведены примеры таких дробей:

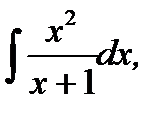
1. неправильная рациональная дробь.

2. неправильная рациональная дробь.

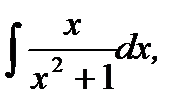
3. 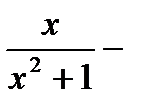правильная рациональная дробь.

Отметим, что в случае неправильной рациональной дроби мы делим многочлен на многочлен столбиком и приходим к сумме целой части и правильной рациональной дроби. Ниже показаны примеры деления многочлена на многочлен столбиком:

1.

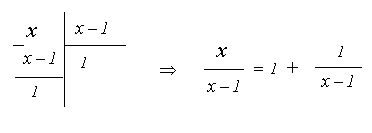
2.

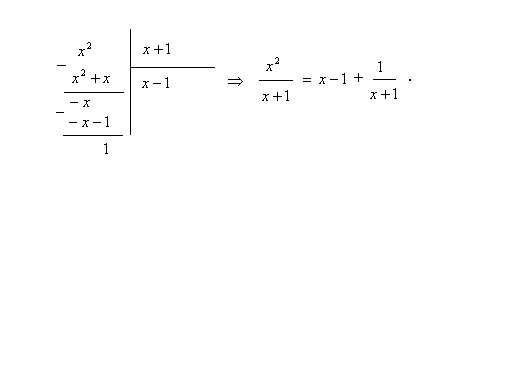
3.

4.

Если знаменатель правильной рациональной дроби можно представить в виде произведения линейных двучленов и квадратных трехчленов (в случае, когда они не имеют действительных корней) в различных степенях, то эту дробь можно представить как сумму правильных рациональных дробей с неопределенными коэффициентами (метод Лагранжа). Например,

(5.29)

Неопределенные коэффициенты Лагранжа находим следующим образом: правую часть (5.29) приводим к общему знаменателю и приравниваем числители правой и левой частей (5.29). Далее пользуемся известной теоремой линейной алгебры: два многочлена одинаковой степени тождественно равны, если равны коэффициенты при одинаковых степенях 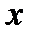слева и справа. Из полученной системы линейных уравнений находим неопределенные коэффициенты Лагранжа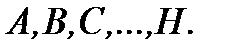

Пример 5.21.Вычислить неопределенный интеграл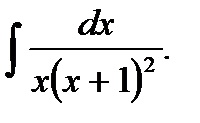

Решение.

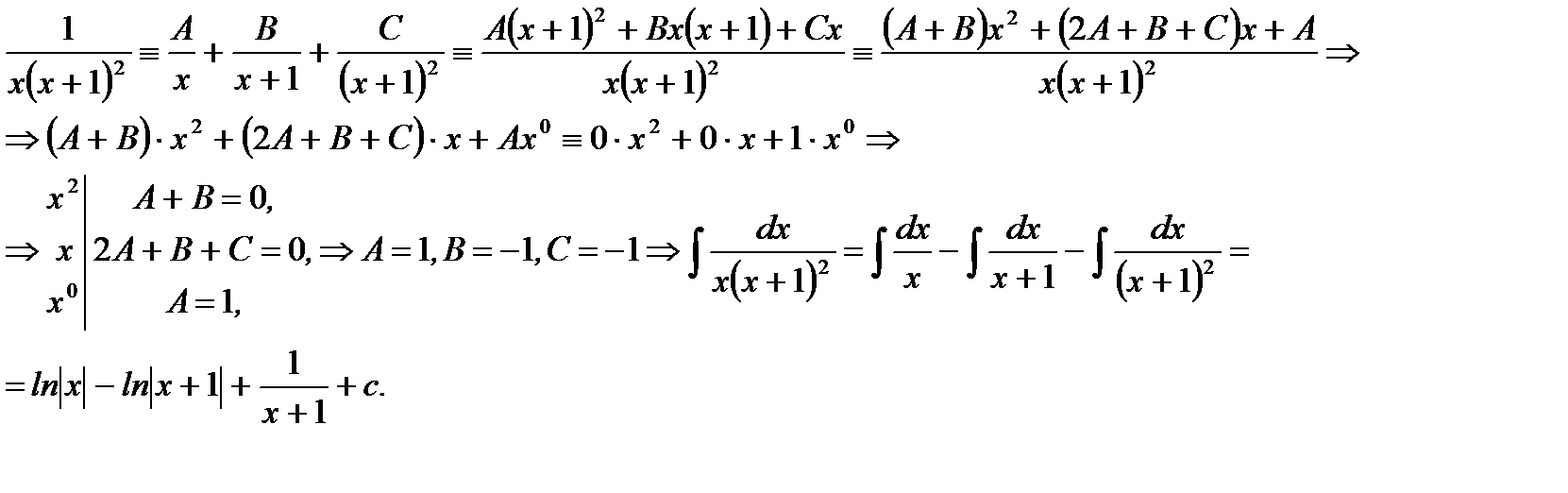
Ответ: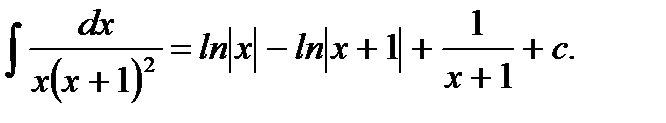

Пример 5.22.Вычислить неопределенный интеграл

Решение.Учитывая, что

имеем

(5.30)

Второй интеграл в правой части (5.30) вычислим методом Лагранжа. Для этого подынтегральную функцию представим в виде суммы правильных рациональных дробей с неопределенными коэффициентами и вычислим эти коэффициенты. Итак, имеем

Ответ: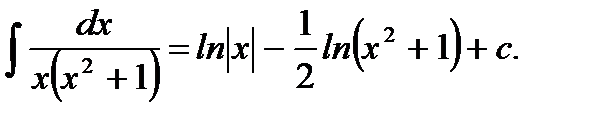

Пример 5.23.Вычислить неопределенный интеграл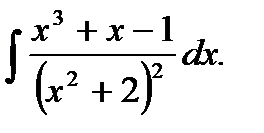

Решение.

(5.31)

Отметим, что вычислили по рекуррентной формуле (5.24).

Ответ:

Пример 5.24.Вычислить неопределенный интеграл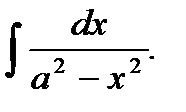

Решение.

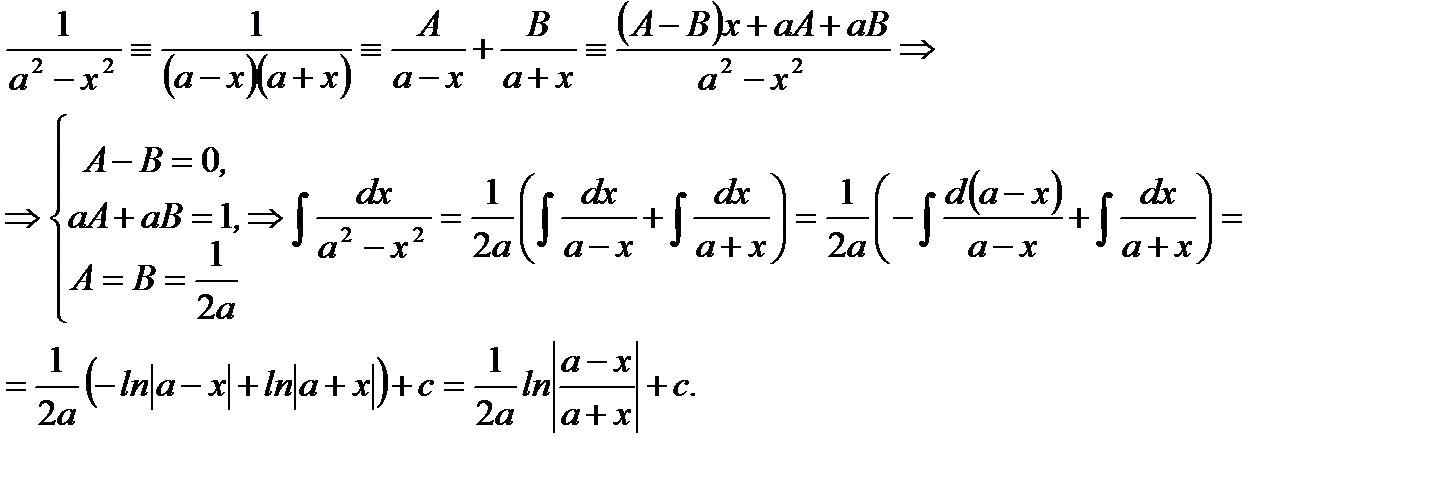
Ответ: (5.32)