Несобственный интеграл первого рода и его вычисление.
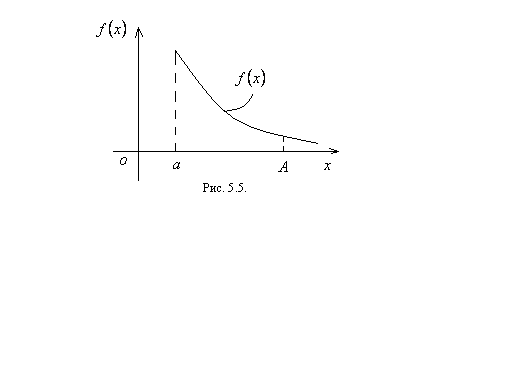
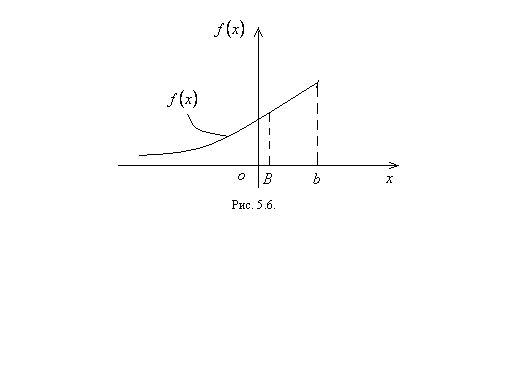
Если подынтегральная функция в определенном интеграле непрерывная (тогда она ограничена), а один из пределов или оба предела бесконечные, то имеем дело с несобственным интегралом первого рода (см. рисунки 5.5, 5.6, 5.7). Способ вычисления несобственного интеграла первого рода приведен ниже.
1. 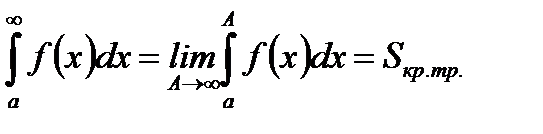 (5.53)
(5.53)
2. 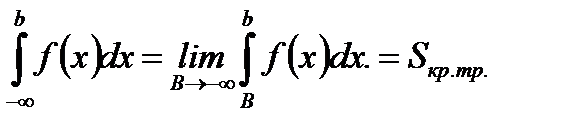 (5.54)
(5.54)
3. 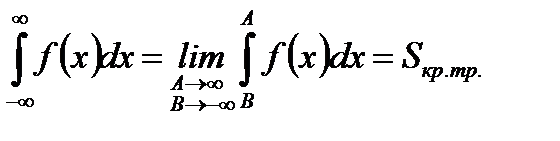 (5.55)
(5.55)
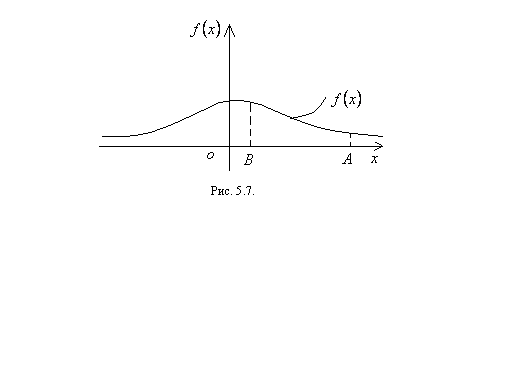
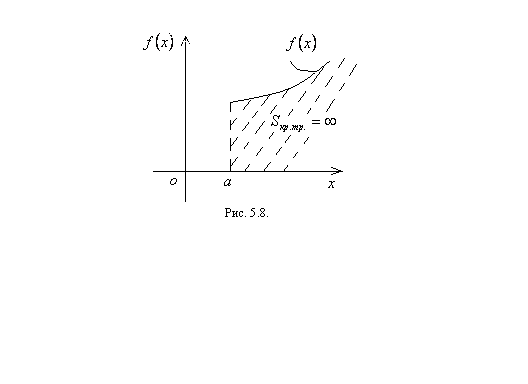
Если в результате вычисления пределов (5.53) – (5.55) получаем конечные числа, то говорим, что несобственный интеграл первого рода сходится, а если получаем бесконечность или вообще нет пределов, то говорим, что несобственный интеграл расходится. Заметим, что несобственный интеграл первого рода, как определенный интеграл, геометрически определяет площадь криволинейной трапеции (см. рисунки 5.5 – 5.7). Если несобственный интеграл сходится, то площадь криволинейной трапеции конечное число, а если расходится, то площадь криволинейной трапеции бесконечно большое число или вообще не определяется. Очевидно, что, если 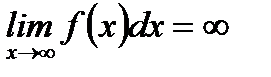 (см. рисунок 5.8), то
(см. рисунок 5.8), то 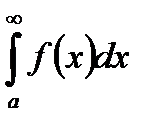 расходится, то есть площадь криволинейной трапеции стремится к бесконечности.
расходится, то есть площадь криволинейной трапеции стремится к бесконечности.
Теорема 5.1.Для сходимости 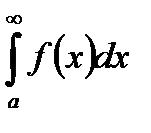 необходимо выполнение условия
необходимо выполнение условия 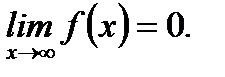
Суть этой теоремы в том, что, если 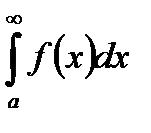 сходится, то следует, что подынтегральная функция на бесконечности стремится к нулю. Но из выполнения условия
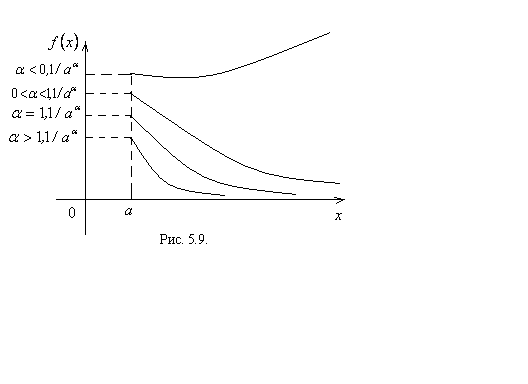
сходится, то следует, что подынтегральная функция на бесконечности стремится к нулю. Но из выполнения условия 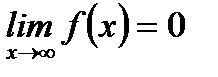 не следует сходимость несобственного интеграла. Оказывается, что сходимость или расходимость несобственного интеграла зависит от того, по какому правилу или закону подынтегральная функция на бесконечности стремится к нулю. Для выяснения этого вопроса рассмотрим поведение несобственного интеграла первого рода от функции
не следует сходимость несобственного интеграла. Оказывается, что сходимость или расходимость несобственного интеграла зависит от того, по какому правилу или закону подынтегральная функция на бесконечности стремится к нулю. Для выяснения этого вопроса рассмотрим поведение несобственного интеграла первого рода от функции 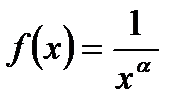 при различных значениях
при различных значениях 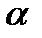 (см. рисунок 5.9).
(см. рисунок 5.9).
1. 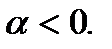
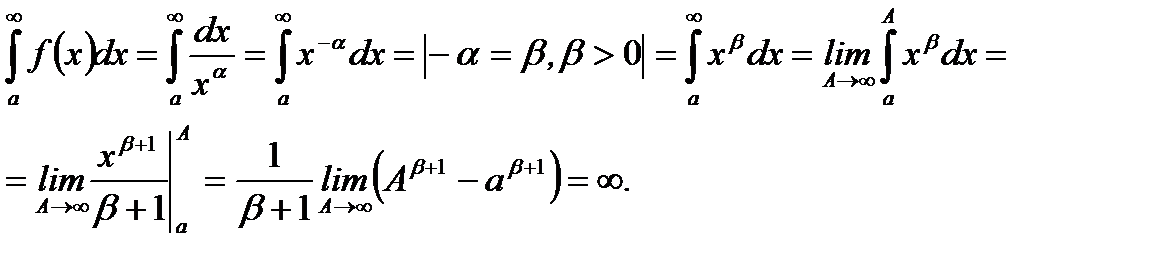 (5.56)
(5.56)
(5.56) показывает, что в случае  несобственный интеграл первого рода расходится.
несобственный интеграл первого рода расходится.
2. 
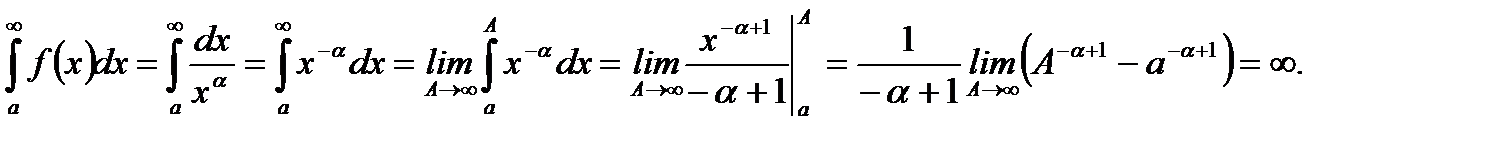 (5.57)
(5.57)
(5.57) показывает, что в случае 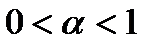 несобственный интеграл первого рода расходится.
несобственный интеграл первого рода расходится.
3. 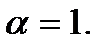
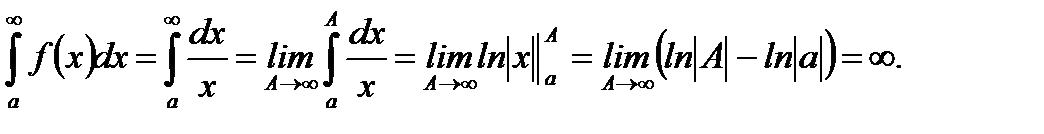 (5.58)
(5.58)
(5.58) показывает, что в случае 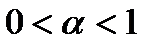 несобственный интеграл первого рода расходится.
несобственный интеграл первого рода расходится.
4. 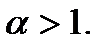
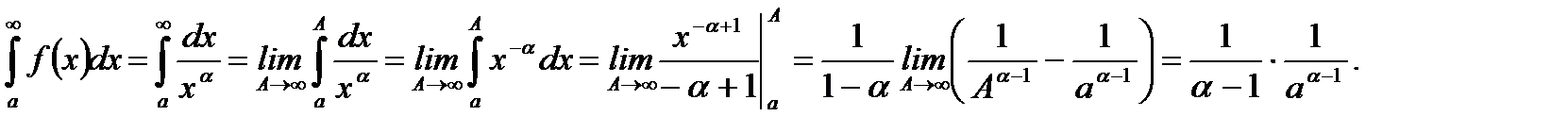 (5.59)
(5.59)
Так как в результате вычисления интеграла получили конечное число (см. (5.59)), то в этом случае несобственный интеграл первого рода сходится.
Пример 5.52.Вычислить интеграл
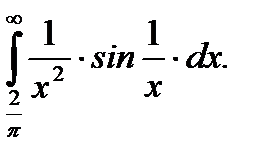
Решение.
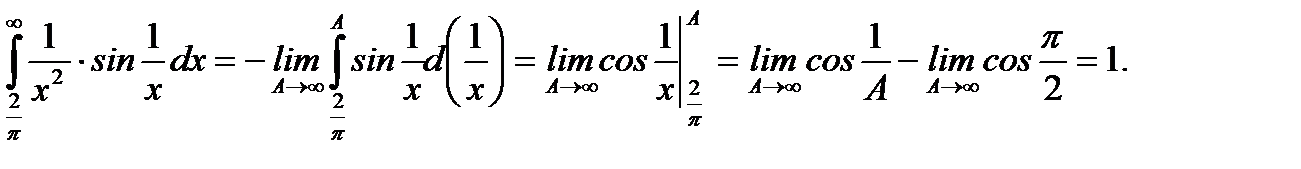
Ответ:интеграл сходится и 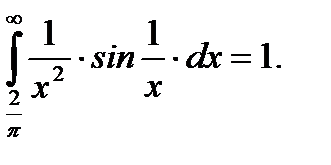
Дата добавления: 2021-05-28; просмотров: 403;











