Два интегрирующих звена.

Отрезок покоя |x|≤a является абсолютно устойчивым, если выполняются следующие условия:

1. Функция N(x) непрерывна и удовлетворяет условиям:

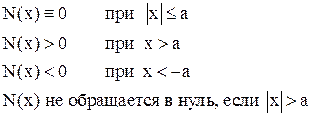
2. При разложении на простые дроби должны быть положительными коэффициенты при p в минус второй и минус первой степени:

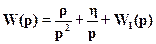
W₁(p) содержит все слагаемые разложения на простые дроби, имеющие полюса в левой полуплоскости.

3. Выполняется неравенство:

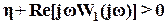(56)

4.

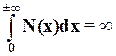
Условие расходимости интеграла заведомо выполняется, если кривая N(x) находится на конечном расстоянии от оси абсцисс.

Замечание.

Если сравнить условия устойчивости отрезка покоя и точки покоя, то основным изменением является то, что должно выполняться неравенство (56), а не неравенство В.М.Попова. Величина μ₀ не имеет значения в теореме об устойчивости точки покоя, так как прямая В.М.Попова совпадает с действительной осью.

Круговой критерий абсолютной устойчивости нелинейной системы в общем случае S(μ₁, μ₂) и в базовом случае S(μ₀).

Для применения кругового критерия используется не модифицированная частотная характеристика, акривая Найквиста. На свойства нелинейной функции N(x) накладываются минимальные ограничения: N(x) может быть гистерезисной функцией, иметь зону нечувствительности и разрывы первого рода. Основное условие – нахождение внутри сектора (см. рис. 11).

Пусть ЛСС устойчива по критерию Найквиста для всех значений коэффициента усиления μ, удовлетворяющих неравенству:

μ₁ < μ < μ₂

Очевидно, что кривая Найквиста не может пересекать отрезок[-μ₁^-1,-μ₂^-1]. Построим на этом отрезке как на диаметре окружность.

Круговой критерий утверждает, что для устойчивости положения равновесия или отрезка покоя (зоны нечувствительности) нелинейной системы достаточно, чтобы кривая Найквиста не пересекала и не касалась построенной окружности.

Обратим внимание, что при стремлении μ₁ к нулю (μ₂ фиксировано),точка -μ₁^-1будет неограниченно перемещаться влево по отрицательной части действительной оси к бесконечности. При этом окружность будет бесконечно увеличиваться и в пределе перейдёт в горизонтальную прямую, параллельную мнимой оси, проходящую через точку μ₂. Поэтому для нелинейности в секторе S(μ₀) круговой критерий имеет следующий вид:

μ₀^-1 + Re(W(j ω))>0 (30)

Неравенство (30) назовем неравенством В.А.Якубовича.

Круговой критерий не требует стационарности блока N, поэтому возможно его применять к линейной нестационарной функции

u = a(t)x (31)

при условии, что функция a(t) не выйдет за границы сектора.

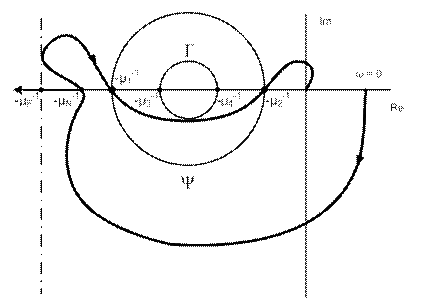
Рис. 26

Обратимся к рисунку 26, где построена кривая Найквиста для некоторой устойчивой передаточной функции W(p). Рассмотрим вопрос об определении границ устойчивости нелинейной системы. Обратим внимание, что, если границы устойчивости линейной системы определяются однозначно, то границы сектора абсолютной устойчивости по круговому критерию определяются неоднозначно. Например, линейная система будет устойчива при μ₁ < μ < μ₂ .

Круговой критерий не удовлетворяется для сектора S(μ₁, μ₂), так как соответствующая окружность Ψ пересекает кривую Найквиста. Для сектора S(μ₃, μ₄) круговой критерий удовлетворяется, окружность Γ не пересекает кривую Найквиста. Но числа μ₃, μ₄ можно выбрать различным образом внутри отрезка [μ₁, μ₂]. В том случае, если нелинейность находится в базовом секторе, максимальное значение, которое мы можем взять, - это μ_F. Обратим внимание, что максимальное значение для сектора линейной системы будет величина μ_N , большая, чем μ_F.