Исследование динамики релейных систем на многолистной фазовой плоскости.

Релейные системы авторегулирования, особенно системы стабилизации, которым посвящен данный параграф, широко используются в технике. Основным способом улучшения качества (повышение точности) в релейных системах второго порядка является использование воздействия по производной. К сожалению, если запаздывание в объекте управления велико, то воздействие по производной не может привести к существенному улучшению процесса стабилизации.

Постановка задачи.

· Передаточная функция объекта вместе с исполнительным устройством в общем случае имеет вид:

W(p) = 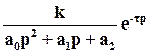(1)

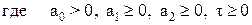
Отметим, что согласно принятым ограничениям на коэффициенты передаточная функция W(p) может содержать только устойчивые и нейтральные звенья.

· В качестве регулятора в системе используется релейный элемент (симметричный).

· Предполагается, что кроме выходной координаты объекта x возможно измерить или вычислить с допустимой точностью её производную y = x’.

· При изучении динамики системы мы ограничимся только ее собственными движениями.

Структурная схема системы показана на рисунках 1 и 2, где вектор х⁰ символически обозначает начальные условия, т.е. исходное положение объекта (х₀, y₀). Неотрицательная величина f на структурной схеме (рис. 1) называется коэффициентом воздействия по производной.

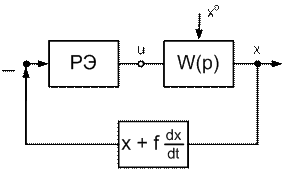
Рис.1

Система управления в общем случае описывается уравнением:

a₀x''(t) + a₁x'(t) + a₂x = -ku[x(t – τ) + f·x'(t - τ)] (2)

Правая часть дифференциального уравнения 2 является функцией, которая в зависимости от значения ее аргумента может принимать только три фиксированных значения:

-kс, 0, +kс

Если в качестве регулятора используется двухпозиционное реле, то функция в правой части принимает только два фиксированных значения:

-kc, +kc

Замечание.

Случай, когда W(p) содержит два интегрирующих звена, позволяет наиболее просто и наглядно исследовать разнообразные динамические процессы важные для понимания теории нелинейных систем, поэтому ему уделяется значительное место в данном параграфе.

В практическом отношении исключительно важен случай, когда W(p) содержит апериодическое и интегрирующее звенья.

2. Общие вопросы изучения динамики релейной системы на фазовой плоскости. Многолистная фазовая плоскость.

Целесообразно изучать динамику системы на фазовой плоскости, когда величина в правой части дифференциального уравнения системы постоянна. Поэтому введем понятие многолистной фазовой плоскости.

На каждом листе многолистной фазовой плоскости динамика системы будет описываться линейным дифференциальным уравнением, правая часть которого const.

Для изучения динамики на фазовой плоскости от уравнения (2) переходят к системе уравнений первого порядка.

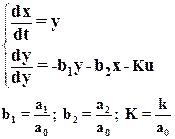(3)

Делим в системе (3) второе уравнение на первое и получаем уравнение фазовых траекторий:

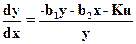(4)

Замечание.

Отметим, что если коэффициент b₂ в уравнении (4) равен нулю, то уравнение изоклин траекторий на фазовой плоскости будет горизонтальная прямая. Такой случай будет иметь место, когда W(p) состоит из двух интегрирующих звеньев или одного интегрирующего и одного апериодического звена. Все фазовые траектории можно получить с помощью сдвига или поворота одной траектории, т.е. можно сделать шаблон по одной траектории и затем с его помощью построить весь фазовый портрет (ось шаблона должна быть совмещена с осью абсцисс фазовой плоскости).