Конструирование многолистной фазовой плоскости в зависимости от типа релейного элемента.

2.1. Запаздывание равно нулю, и воздействие по производной так же равно нулю (τ = 0, f = 0).

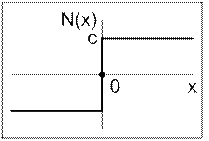
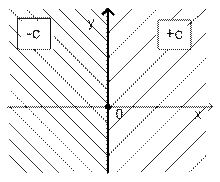
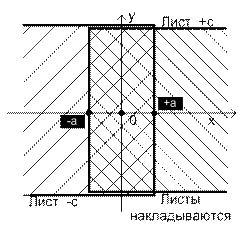
· Начнем со случая двухпозиционного реле. Рассмотрим три фазовые плоскости с одинаковым масштабом. На первой плоскости выделим ту часть, когда сигнал реле u равен +c и вырежем ее. Эту часть фазовой плоскости назовём листом «+c». На второй фазовой плоскости выделим ту часть, где сигнал реле u равен –c. Вырежем ее и назовем листом «-c». Затем оба листа наложим на исходную фазовую плоскость. Если реле не имеет гистерезиса, то границы листов сомкнутся. В том случае, когда реле имеет гистерезис, листы наложатся друг на друга. Если реле не имеет гистерезиса, то переход изображающей точки с одного листа на другой происходит по границе листов.

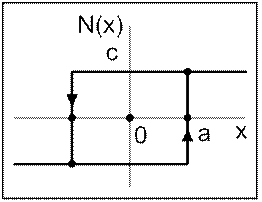
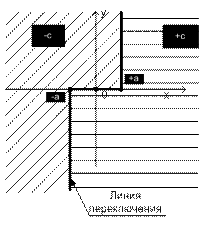
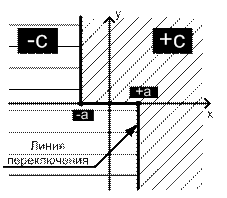
В случае, когда реле имеет положительный гистерезис, переход изображающей точки с листа на лист жёстко определён двумя условиями:

1) |x| = a;

2)направление переключения реле однозначно определяется знаком производной: y = x'.

Линию перехода изображающей точки с одного листа на другой условимся называть линией переключения

Реле. Фазовая плоскость.

a)

b)

Рис. 2

Реле. Фазовая плоскость.

a)

b)

Фазовая плоскость.

с)

Рис. 3

Упражнение. Исследовать структуру фазовой плоскости, если реле имеет три позиции (+с, 0, -с).

Пояснение.

Аналогично предыдущему мы получаем трёхлистную фазовую плоскость. Если реле имеет гистерезис, то листы фазовой плоскости налагаются друг на друга.

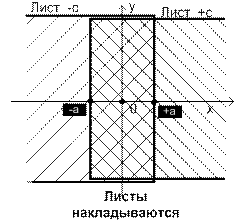
· Реле с опережением (с отрицательным гистерезисом).

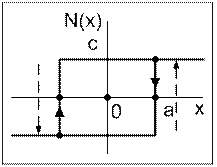
Теперь перейдём к случаю реле с опережением (с отрицательным гистерезисом). Начнем рассмотрение с двухпозиционного реле. В этом случае, очевидно, листы налагаются друг на друга, как показано на рисунке 4.

Вопрос о линии переключения в случае использования реле с опережением более сложен, чем в случае обычных гистерезисных реле. В точках |x| = a возможно переключение реле в зависимости от знака производной y = x' в противоположных направлениях (с –с на +с, или наоборот). Линия переключения может иметь вид, показанный на рисунке 4с, но может и совпадать с границей листа, как будет показано в дальнейшем.

Реле. Фазовая плоскость.

a)

b)

Фазовая плоскость.

с)

Рис. 4

Упражнение. Построить разбиение фазовой плоскости на листы в случае трёхпозиционного реле с опережением.

2.2. Запаздывание равно нулю, а воздействие по производной больше нуля (τ = 0, f > 0).

В этом случае линии переключения будут определяться уравнениями:

для двухпозиционного реле.

y + f·x = 0 (5)

для трёхпозиционного реле.

y + f·x = ±a (6)

воздействие по производной приводит к тому, что границы листов наклоняются в соответствии с соотношениями (5) и (6).

Отметим, что наклон линий переключения может привести к явлению, которое называется скольжением. Это явление будет рассмотрено ниже.

Запаздывание.

Влияние запаздывания на свойства системы скажется в том, что сигнал реле будет переключаться с опозданием на время τ. В течение промежутка времени τ изображающая точка будет двигаться по старой траектории, таким образом, запаздывание не изменит формы фазовых траекторий на листах, но деформирует вправо линии переключения изображающей точки с одного листа на другой, что разумеется, может приводить к кардинально новым явлениям (по сравнению с тем случаем, когда запаздывание отсутствует), например, к возникновению автоколебаний.