Приведение дифференциального уравнения системы к простейшей форме.

С помощью масштабирования по переменной х и масштабирования по времени дифференциальное уравнение системы может быть преобразовано к, так называемой, простейшей форме (к простейшему виду). Под термином «простейшее» понимается такая форма записи дифференциального уравнения системы, которая содержит минимальное число параметров.

Масштаб по переменной условимся обозначать буквой m, а масштаб по времени – буквой μ.

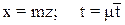(7)

В рассматриваемых ниже примерах величина μ равна или постоянной времени T, или .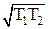

Сигнал на выходе релейного элемента u будем записывать в виде:

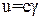(8)

Где функция γ принимает значения: -1,+1 или -1, 0, +1.

Для краткости опускаем запись аргументов у релейных функций u и γ.

Применение масштабирования приводит к необходимости следующих изменений:

1. Параметры релейного элемента а и b заменяются величинами

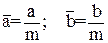(9)

2. Время запаздывания τ заменяется величиной:

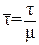(10)

3. коэффициент воздействия по производной f заменяется величиной:
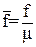(11)

Напомним, как изменяется k-тая производная функции при масштабировании по времени:

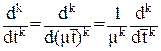(12)

· Отметим очень важное обстоятельство.

Исследовать дифференциальное уравнение в простейшей форме легче, чем исходное, т.к. оно содержит меньше параметров, а задача часто состоит в том, чтобы определить, как изменяются свойства решения дифференциального уравнения системы в зависимости от изменения параметров.

Качественные закономерности решений исходного уравнения и уравнения в простейшей форме, очевидно, совпадают, так как мы можем однозначным образом перейти от масштабированных данных к исходным.

4. Исследование динамики релейной системы управления объектом, имеющим передаточную функцию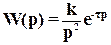

Дифференциальное уравнение системы имеет вид:

x'' = -ku (13)

уравнение фазовых траекторий:

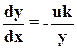(146)

Его решение можно записать в форме:

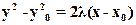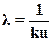; (15)

или

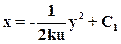(16)

Где С₁ – постоянная интегрирования.

Графики траекторий при u = +c показаны на рисунке 5 a, а при u = -c - на рисунке 5 b, при значении постоянной интегрирования С₁=0. сдвигая эти параболы как жёсткое целое вдоль оси абсцисс, мы можем получить любую траекторию.

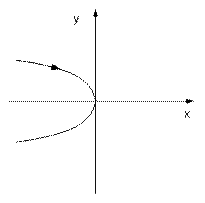a)

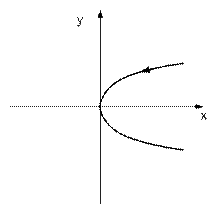b)

Рис. 5

· Начнем рассмотрение фазовых портретов для случая, когда воздействие по производной отсутствует, т.е. f=0.

Фазовый портрет системы для двухпозиционного реле без гистерезиса показан на рисунке 6, и для трёхпозиционного - на рисунке 7.

Рис.6

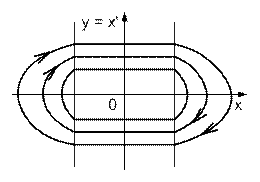Рис.7

Фазовый портрет представляет собой в обоих случаях бесконечное семейство вложенных друг в друга замкнутых кривых (внимание! не путать с предельным циклом!).

Фазовый портрет для двухпозиционного реле с гистерезисом показан на рисунке 8. В данном случае в системе имеют место расходящиесяколебания.

Рис.8

Рассмотрим случай двухпозиционного реле с опережением.

В этом случае процесс свободных колебаний в системе имеет весьма специфические свойства. В какой бы точке фазовой плоскости не находилась в исходный момент изображающая точка, в процессе своего движения, она придет на некоторую замкнутую линию Г, по которой и будет совершать движение при t→∞. Форма замкнутой линии Г зависит от начальных условий, поэтому линия Г не является предельным циклом. Можно только сказать, что в любом случае линия Г будет иметь осью симметрии одну из границ листов. Движению изображающей точки по линии Г соответствует во временной области незатухающие колебания, но эти колебания не являются автоколебаниями!!

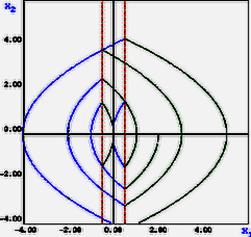
Рис. 9

Сколь бы далеко ни находилась изображающая точка от начала координат, она будет двигаться к одной из двух замкнутых линий, имеющих оси симметрии – прямые x =a и x =-a (внимание! эти замкнутые линии не являются предельными циклами!).

· Перейдем к рассмотрению случая, когда имеет место воздействие по производной, т.е. f>0.

В этом случае линии переключения наклоняются. Возможна ситуация, когда, переходя с одного листа на другой, изображающая точка не сможет двигаться по новому листу, т.к. соответствующая траектория уходит за его границу. В этом случае изображающая точка начнет двигаться по самой линии переключения(как показано на рисунке 10 и 11),что физически будет соответствовать колебаниям с бесконечной амплитудой, как показано на рисунке 10. (Строго говоря, в этой ситуации мы должны доопределить понятие решения дифференциального уравнения, что и делается в полных курсах теории управления. Обычно решение доопределяется в соответствии с теорией А.Ф.Филипова (профессор МГУ)).

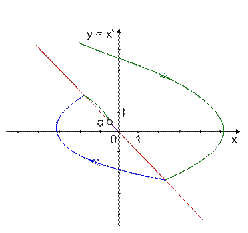Рис.10	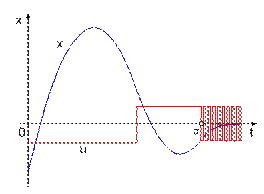Рис.11
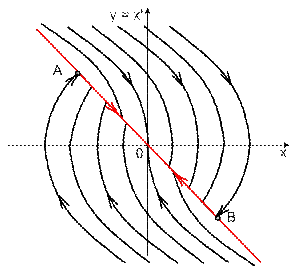Рис.12

АВ – отрезок скольжения на линии переключения.