Выясним, как отображаются на фазовой плоскости различные функции времени.

С этой целью рассмотрим несколько примеров.

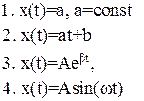(1)

Для построения графика на фазовой плоскости вычислим функцию y=f(x) или неявную функцию g(x,y)=0.

1. y = x’ = 0, следовательно, на фазовой плоскости имеем точку с координатами (а, 0).

2. у = х’ = а, следовательно, изображающая точка по фазовой плоскости будет двигаться по горизонтальной прямой, параллельной оси абсцисс.

3. y = x’ = 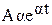, находим отношение: 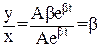, следовательно y=βx. Таким образом, движение по экспоненте во временной области соответствует движению по прямой, проходящей через начало координат на фазовой плоскости (см. рис. 1).

Рис. 1

Направление движения на фазовой плоскости однозначно определяется условием, что если y>0, х должен возрастать, а если y<0, х должен убывать, так как у – производная от х.

4. Сначала рассмотрим случай ω = 1.

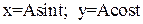(2)

Возведём х и у в квадрат и сложим:

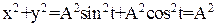(3)

Следовательно, гармоническому колебанию при ω = 1 на фазовой плоскости соответствует движение по окружности.

Рассмотрим общий случай: ω≠1.

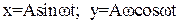(4)

Домножим х на ω и вычислим сумму квадратов:

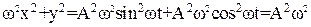(5)

Отсюда получаем:

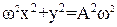(6)

Это уравнение эллипса. Приведем его к канонической форме:

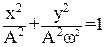(7)

Следовательно, гармоническое колебание соответствует движению по эллипсу на фазовой плоскости (см. рис. 2).

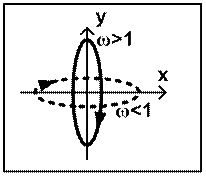
Рис. 2

5. Рассмотрим более сложный случай затухающих и расходящихся колебаний.

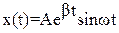(8)

Продифференцируем это выражение:

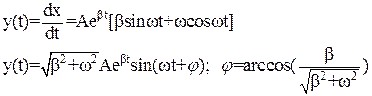(9)

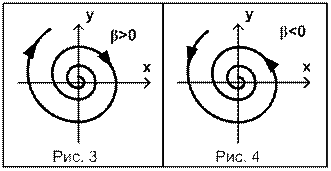
Колебаниям, описанным функцией x(t) соответствует на фазовой плоскости движение по спирали. Если β<0, то спираль будет закручиваться и сходиться к нулю, а если β>0, то спираль будет раскручиваться и уходить в бесконечность.

Действительно, пусть в фиксированный момент времени t₀ имеем:

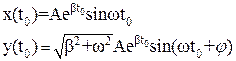(10)

Через интервал времени 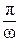, т.е t₁ = t₀ + 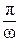, значения функций будут равны:

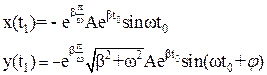(11)

Сопоставляя формулы (10) и (11), мы видим, что вектор, соответствующий изображающей точке, повернулся на 180º (х и у поменяли знак), а длина вектора умножилась на величину 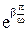. Если β отрицательно, то эта величина меньше единицы, и вектор «сжался», а если β положительно, то вектор, естественно, удлинился.

2. Вычисление интервала времени при движении по фазовой траектории.

Пусть фазовая траектория y = f(x). Определим время, за которое она пройдет расстояние от точки а до точки b (a>0, b>0)

а = f(t₀), b = f(t₁)

записываем соотношение:

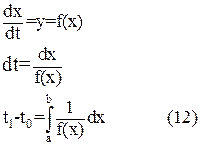
Из формулы (12) следует, что интервал времени равен площади под кривой 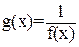. Очевидно, что чем выше проходит кривая, соединяющая точки а и b, тем за меньшее время изображающая точка переместится из точки а в точку b.

Формула (12), формально говоря, может быть использована для определения времени по фазовой траектории. Но практически ее редко удается применить – возникают сложности с вычислением интеграла.