Динамика нелинейных систем автоматического управления.

В учебном пособии рассмотрены два подхода к исследованию динамики нелинейных САУ.

Первый метод – метод фазового пространства (метод пространства состояния), который позволяет провести полное исследование системы, но, к сожалению, очень сложен даже при наличии современных ПК.

Второй метод - применение частотных методов исследования динамики нелинейных САУ. Этот метод отличается простотой и наглядностью, но позволяет провести лишь частичный анализ.

Глава 11. Методы фазового пространства.

Основные понятия теории устойчивости.

Предположим, что нелинейная система управления описывается системой обыкновенных дифференциальных уравнений с постоянными коэффициентами.

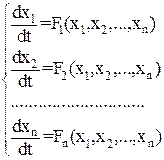(1)

Системы такого вида называют динамическими системами.Название это заимствовано из механики.

Предположим, что функции F_k и их производные по всем переменным х_j непрерывны.

Используя векторную запись, условимся обозначать:

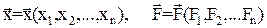(2)

Система (1) можно кратко записать:

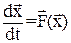(3)

Решение системы: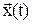

Вектор начальных условий: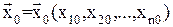

Решение системы (1) однозначно определяется вектором начальных условий, заданных в некоторый момент времени t = t₀. (Обычно t₀ = 0).

Поэтому более наглядной является обозначение: 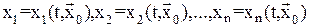(4)

Или короче:

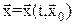(5)

Замечание.

Сформулированные ограничения на функции F_k являются часто слишком жёсткими для систем автоматического управления. Во многих случаях необходимо рассматривать функции F_k , являющиеся кусочно-линейными, разрывными и даже неоднозначными.

Тем не менее, целесообразно начать изучение системы (1) с вышеприведенных, общепринятых в математике классических ограничений для функции F_k, так только в этом случае разработана общая теория.

Рассмотрим некоторые фундаментальные понятия в общем виде, затем перейдем к изучению нелинейных систем второго порядка вида (6)

Отметим, что фактически изучение нелинейных систем мы начнём со случая системы второго порядка:

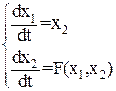(6)

· Фазовое пространство.

Пространство переменных х₁, х₂, …, х_n назовем фазовым пространством,а сами эти переменные – фазовыми переменнымиили фазовыми координатами.

В теории управления последние годы несколько изменилась терминология, и фазовое пространство называют пространством состояния системы (1) соответственно х₁, х₂, …, х_n – переменными в пространстве состояния.Однако в данной работе мы будем придерживаться «фазовой» терминологии.

Пусть функции х₁(t), х₂(t), …, х_n(t) являются решениями системы (1) при изменении t от 0 до ∞. Для фиксированного момента времени t мы получаем набор чисел, определяющих точку в фазовом пространстве. Если рассматриваем процесс при изменении t, то эту точку будем называть изображающей точкой,а линию, которую она прочерчивает в пространстве при изменении t от 0 до ∞, условимся называть фазовой траекторией.

Иначе можно сказать, что каждое решение системы (1) определяет линию в фазовом пространстве, а если все 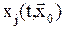постоянные, то оно определяет точку. Эту точку называют «положение равновесия»или «особая точка». Линию, определяемую решением уравнения (1), называют фазовой траекторией.Это же название используется для случая, когда решением является точка. То есть мы получаем траекторию-точку.