Хотя бы один корень характеристического уравнения находится в правой полуплоскости (имеет положительную действительную часть). В этом случае положение равновесия неустойчиво.

3. В правой полуплоскости нет корней характеристического уравнения, но на мнимой оси есть один или несколько корней (остальные находятся в левой полуплоскости). Этот случай Ляпунов назвал критическим. Для суждения об устойчивости использовать линеаризованную систему (10) нельзя. Необходимо использовать нелинейные члены при разложении функции F_k в ряд.

Необходимо подчеркнуть, что в приведенной теореме под устойчивостью положения равновесия понимается только тот факт, что существует некоторая окрестность ρ, внутри которой решение системы (1) устойчиво, но величина этой окрестности не вычисляется и она может быть весьма малой!

Выше мы обсудили понятие устойчивости положения равновесия в малом, теперь сформулируем еще несколько важных определений понятия устойчивости положения равновесия.

Предположим, что положение равновесия устойчиво в некоторой области G, границы которой нам известны. В этом случае говорят, что положение равновесия устойчиво в большом. Область G может быть невелика, но, разумеется, может быть и очень большой. В соответствии с русским языком, наверное, более уместно было бы говорить об устойчивости в конкретной области, однако, терминология в математике такова, и мы, естественно, будем ей пользоваться.

Пусть система (1) имеет единственное положение равновесия (m = 1) и это положение равновесия устойчиво во всем n-мерном фазовом пространстве.

В этом случае положение равновесия называется устойчивым в целом.

Если единственное положение равновесия асимптотически устойчиво в целом, то говорят, что оно является точкой притяжениядля всего фазового пространства.

Подводя итог приведенным определениям устойчивости положения равновесия, обратим внимание, что устойчивость по Ляпунову по смыслу задачи можно назвать – устойчивостью по начальным отклонениям.

2)Применение функции Ляпунова для исследования устойчивости положения равновесия.

Под функцией Ляпунова понимают следующее. Рассмотрим функцию всех фазовых переменных 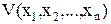или сокращенно 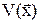. Наряду с функцией V 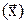введем в рассмотрение функцию 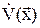, которая является производной функции V в силу системы уравнений(1).

Вычисляем производную функции V:

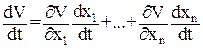(24)

Затем производные функций х_i(t) заменяем правыми частями в уравнении (1) – функциями F_i . Получаем:

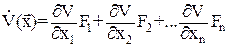(25)

Предположим, что существует область G, внутри которой функция V является дифференцируемой по всем координатам х_i.

Теорема Ляпунова утверждает, что нулевое решение устойчиво по Ляпунову, если в области G выполняются следующие условия:

а) V(0) = 0, 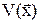>0, если ;

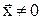b) 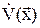≤0

Нулевое решение будет асимптотически устойчиво по Ляпунову, если в условии b) заменить нестрогое равенство на строгое, т.е.

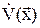<0.

Замечание.

В 1953 году советскими математиками Е.А.Барбашиным и Н.Н.Красовским было показано, что на функцию Ляпунова целесообразно наложить ещё одно ограничение, кроме указанных выше.

Функция Ляпунова должна еще удовлетворять условию, что 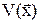→∞, если любая из переменных х_i стремится к бесконечности.

Например, рассмотрим функцию:

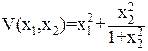
если х₁→∞, то V→∞; но если х₂→∞, то V не будет стремиться к бесконечности, поэтому функция V(x₁, x₂) не целесообразно использовать в качестве функции Ляпунова.

Не приводя доказательство теоремы Ляпунова, поясним идею функций Ляпунова некоторыми простыми соображениями.

Пусть рассматривается трехмерная система (1) n = 3 и исследует устойчивость нулевой точки покоя.

В фазовом пространстве расстояние изображающей точки от начала координат равно:

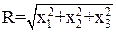(26)

Определим, как движется изображающая точка во времени. Увеличивается ли расстояние от начала координат (точки покоя) или уменьшается? Вычислим производную:
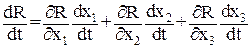(27)

Так как мы рассматриваем движение толькопо траекториям системы, то производные функции х_i(t) нужно заменить функциями F_i(x₁, x₂, x₃)

Получаем:

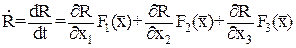(28)

Очевидно, что функция R(x₁, x₂, x₃) положительна всюду кроме точки начала координат, где она равна нулю.

Если ее производная 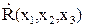отрицательна внутри шара радиуса R₁, то, очевидно, из любой точки этого шара изображающая точка будет постепенно двигаться по траектории к началу координат, так что ее расстояние будет убывать. Начало координат устойчиво.

Если 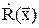положительно, то изображающая точка будет постоянно уходить от начала координат внутри шара R₁. начало координат неустойчиво.

К сожалению, функция 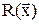может иметь только очень ограниченное применение, так как изображающая точка может стремиться к началу координат, но ее расстояние будет изменяться немонотонно, и функция 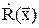будет менять знак.

Чтобы преодолеть эту трудность и вводится функция Ляпунова, для которой предполагается, что ее производная неполжительнана всехтраекториях, ведущих к началу координат.

Метод функций Ляпунова имеет следующий геометрический смысл.

Пусть R – некоторое положительное число. Шар радиуса R находится внутри области G. Соотношение:

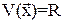(29)

Определяет замкнутую поверхность в области G.

Если во всех точках этой поверхности (29) производная функции Ляпунова отрицательна, то все траектории решения системы (1), проходящие через поверхность (29), направлены вовнутрь (изображающая точка движется к началу координат). В том случае, когда производная функции Ляпунова положительна во всех точках поверхности (29), то траектории направлены вовне (изображающая точка движется от начала координат).

Поэтому если производная функции Ляпунова положительна в области G, то начало координат неустойчиво в большом (то есть в границах области G).

Поясним на примере один вопрос, связанный с выбором области.

Рассмотрим систему уравнений:

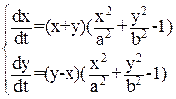(30)

Исследуем устойчивость положения равновесия этой системы х = у = 0. В качестве функции Ляпунова возьмем функцию

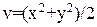(31)

Эта функция принимает положительные значения во всех точках фазовой плоскости кроме начала координат, где она равна нулю.

Вычислим ее производную в силу системы (30): 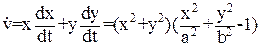(32)

Производная функции Ляпунова (32) отрицательна внутри эллипса

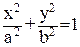(33)

Нам нужно выбрать область, внутри которой будут выполняться два условия:

1) функция Ляпунова положительна;

2) ее производная отрицательна.

Очевидно, что областью G является заштрихованный круг, показанный на рисунке (2).

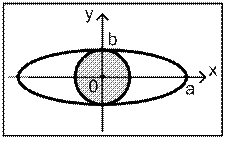
Рис. 2

Приведенный пример показывает, что для определения области G необходимо определить две области. Область G₁, в которой положительна функция Ляпунова, и область G₂, в которой отрицательна ее производная. Область G является общей частью областей G₁ и G₂.

Подведем итог.

1. Функция Ляпунова дает только достаточноеусловие устойчивости положение равновесия в области G. Для одной и той же системы (1) могут быть построены различные функции Ляпунова, определяющие различные области устойчивости. Наибольший интерес представляет, конечно, та функция Ляпунова, которая позволяет определить наибольшую область устойчивости G.

Действительная область устойчивости положения равновесия может быть значительно более широкой, чем область G, так как метод функций Ляпунова определяет достаточное, но не необходимое и достаточное условие (как, например, критерий Гурвица).

2. Неизвестен метод построения функций Ляпунова по заданной системе (1) . Для каждого класса систем дифференциальных уравнений построение функций Ляпунова представляет собой отдельную задачу.

3. Если какое-либо движение (решение системы (1)) является неустойчивым, то физически оно ненаблюдаемое.

· Применение к исследованию устойчивости теории управления.

Впервые применил метод функции Ляпунова для исследования систем автоматического управления ленинградский ученый А.И.Лурье в конце 40-х годов. В 1951 году вышла его книга, которая была переведена на английский язык и положила начало большому числу исследований в СССР, США и других странах.

· Приведем три примера применения функций Ляпунова для исследования устойчивости систем авторегулирования.

Пусть структурная схема систем имеет вид, показанный на рисунках 3, 4, 5:

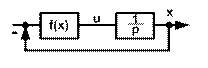
Рис.3 Рис. 4

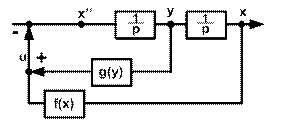
Рис. 5

Функции f(x) и g(y) удовлетворяют следующим условиям:

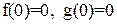
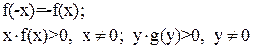(34)

Кроме того интеграл 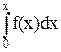стремится к бесконечности при х→∞

Все три системы имеют единственное положение равновесия.

Первая система: х = 0.

Вторая и третья системы: х = 0, y = 0, где y = .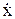

Составим дифференциальное уравнение по каждой из структурных схем.

Для структурной схемы на рисунке 2.

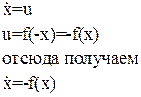(35)

Для структурной схемы на рисунке 3:

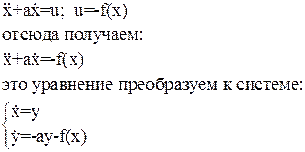(36)

Для структурной схемы на рисунке 4:

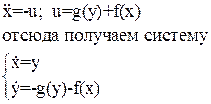(37)

Переходим к исследованию устойчивости положения равновесия в начале координат.

1 система.

Возьмем функцию Ляпунова в виде:

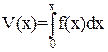(38)

Если х отрицательный, то записываем:

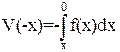(39)

Ясно, что V(x)>0, если х≠0.

Вычисляем производную.

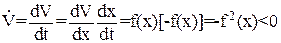(40)

Следовательно, положение равновесия х = 0 асимптотически устойчиво.

2 система.

Функцию Ляпунова берём:

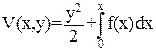(41)

Ясно, что V(x,y)>0, если х≠0, y≠0.

Вычисляем производную.

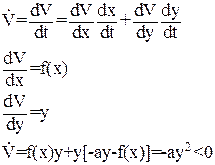(42)

Следовательно, положение равновесия х = 0, y = 0 асимптотически устойчиво.

3 система.

Функцию Ляпунова берем в той же форме, что и во втором примере. Выражения для производной в данном случае

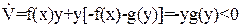(43)

Следовательно, положение равновесия х = 0, y = 0 асимптотически устойчиво.

В трёх разобранных примерах не было задано конкретное аналитическое выражение функций f(x) и g(y). Были наложены только ограничения (12).

Во всех трех примерах функция Ляпунова и ее производная удовлетворяют условиям устойчивости положения равновесия во всем фазовом пространстве (для первой задачи – одномерное пространство, фазовая прямая, для второй и третьей задачи – двумерное пространство, фазовая плоскость).

Следовательно, положение равновесия во всех трех задачах является асимптотически устойчивым во всем фазовом пространстве. В этом случае говорят, что положение равновесия устойчиво в целом.Если учесть, что функции заданы только своими ограничениями (12), а не конкретными выражениями, то мы можем заключить, что положение равновесия абсолютно устойчиво.

Фазовая плоскость.

Рассмотрим частный случай фазовой плоскости. По оси абсцисс будем откладывать значение функций х(t), а по оси ординат – значение ее производной y.