Непрерывность функции

Непрерывные функции.Важный класс функций, изучаемых в М. а., образуют непрерывные функции. Одно из возможных определений этого понятия:

функция y=f(x) от одного переменного х, заданная на интервале ( а, b), называется непрерывной в точке х, если малому приращению аргумента соответствует малое приращение функции, т.е.

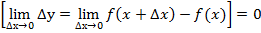
Функция непрерывна на интервале ( а, b), если она непрерывна во всех его точках; тогда ее график представляет собой кривую, непрерывную в житейском понимании этого слова.

Функция 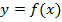непрерывна в точке x=a, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.

Эквивалентные условия:
1. ;
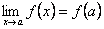2.

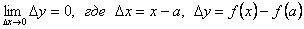
3.
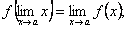
4.
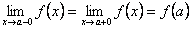
Классификация точек разрыва:

разрыв I рода - устранимый – односторонние пределы существуют и равны;
- неустранимый (скачок) – односторонние пределы не равны;
разрыв II рода: предел функции в точке не существует.
Пример 16. Установить характер разрыва функции в точке x=0 или доказать непрерывность функции в этой точке.

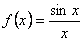
при x=0 функция не определена, следовательно, она не непрерывна в этой точке. т..к.

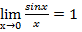и, соответственн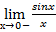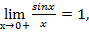о, = то 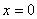– точка устранимого разрыва первого рода.

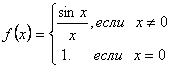
по сравнению с заданием (а) функция доопределена в точке 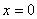так, что 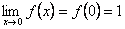, значит, данная функция непрерывна в данной точке.

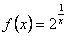
При 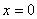функция не определена;

.
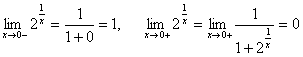т.к. один из односторонних пределов бесконечен, то 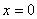– точка разрыва второго рода.