Основные элементарные функции, их свойства и графики.
Элементарные функции.Фундаментальное значение в М. а. играют элементарные функции. На практике в основном оперируют элементарными функциями, ими приближают функции более сложной природы. Элементарные функции можно рассматривать не только для действительных, но и комплексных чисел. Тогда представления об этих функциях становятся в определенном смысле законченными. В связи с этим возникла важная ветвь математического анализа, называемая теорией функций комплексного переменного, или теорией аналитических функций.
Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится.
Перечислим ниже все основные элементарные функции, приведем их графики и дадим без вывода и доказательств свойства основных элементарных функций по схеме:
· область определения функции;
· поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);
· четность и нечетность;
· область значений функции;
· промежутки возрастания и убывания, точки экстремума;
· промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);
· наклонные и горизонтальные асимптоты;
· особые точки функций;
· особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).
Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
· Постоянная функция (константа), ее график и свойства. у=С
· Корень n-о степени, свойства и график. Y= 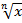
· Степенная функция, ее график и свойства. Y= 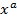
· Показательная функция, свойства, график. Y= 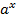
Логарифмическая функция, ее свойства, графическая иллюстрация. Y= 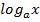 Тригонометрические функции
Тригонометрические функции
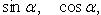
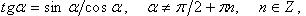
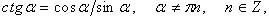
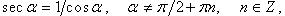
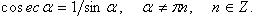
Дата добавления: 2016-06-05; просмотров: 3573;











