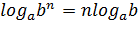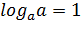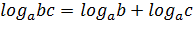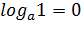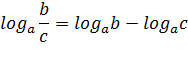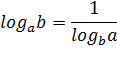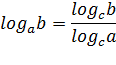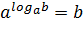Основные тригонометрические тождества
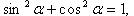
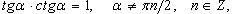
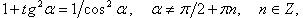
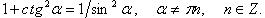
Выражение тригонометрических функций через одну из них того же аргумента
(выбор знака перед корнем зависит от того, в какой четверти находится угол 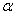 )
)
Через sinx:
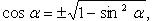
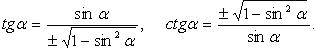
Через cosx:
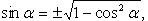
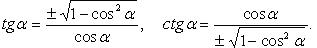
Через tgx:
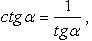
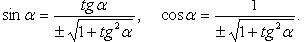
Через ctgx:
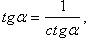
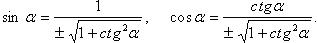
Формулы сложения
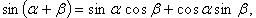
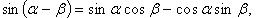
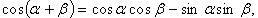
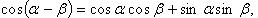
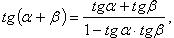
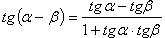
(в последних двух формулах 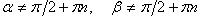 и соответственно
и соответственно 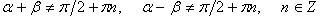 );
);
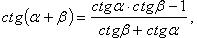
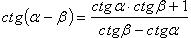
(в последних двух формулах  и соответственно
и соответственно 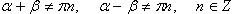 ).
).
Преобразование суммы тригонометрических функций
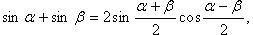
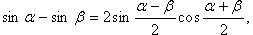
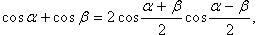
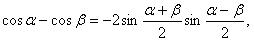
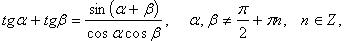
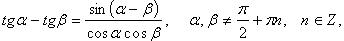
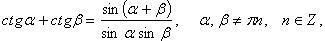
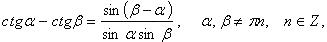
Преобразование произведения тригонометрических функций в сумму
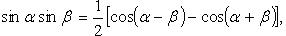
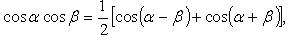
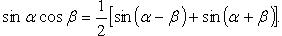
Тригонометрические функции двойного и тройного аргумента
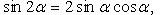
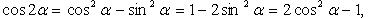
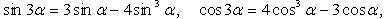
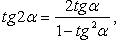
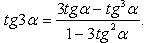
Тригонометрические функции половинного аргумента
(выбор знака зависит от того, в какой четверти находится угол  )
)
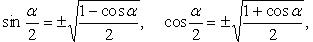
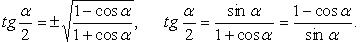
Выражение тригонометрической функции через тангенс половинного аргумента
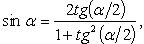
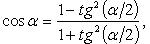
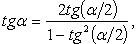
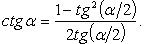
Преобразование степеней синуса и косинуса
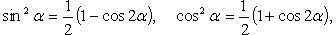
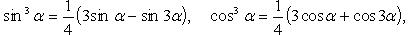
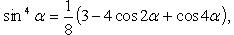
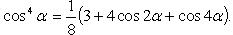
|
II.
·
· Свойства и графики тригонометрических функций. y=sinx, y=cosx, y=tgx, y=ctgx
· Обратные тригонометрические функции (аркфункции), их свойства и графики. 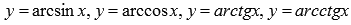
Представление функции может имеет различные формы: в явном виде; в неявном виде; в параметрической форме; разными аналитическим формулами в области определения; графическое; в виде таблиц.
Пример 1. Найти область определения функций.


Действительное число.Понятие функции существенно базируется на понятии действительного (рационального и иррационального) числа. Оно окончательно сформировалось только в конце 19 в. В частности, установлена логически безупречная связь между числами и точками геометрич. прямой, к-рая привела к формальному обоснованию идей Р. Декарта (R. Descartes, сер. 17 в.), к-рый ввел в математику прямоугольные системы координат и представление в них функций графиками.
В математическом анализе методом изучения функций является предел. Различают предел последовательности и предел функции. Эти понятия окончательно сформировались только в 19 в., хотя представление о них имели еще древние греческие ученые.
Определение 1. Пределом функции f(x) при 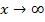 называется число b, если для любого
называется число b, если для любого 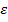 (
( 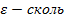 годно малое положительное число) можно найти такое значение аргумента х =
годно малое положительное число) можно найти такое значение аргумента х = 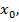 начиная с которого выполняется неравенство
начиная с которого выполняется неравенство 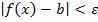 . Обозначение:
. Обозначение: 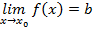
Определение 2. Пределом функции f(x) при 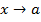 называется число b, если для любого
называется число b, если для любого 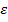 (
( 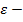 сколь угодно малое положительное число) существует такое положительное число
сколь угодно малое положительное число) существует такое положительное число 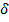 , что для всех значений x, удовлетворяющих неравенству
, что для всех значений x, удовлетворяющих неравенству 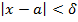 выполняется неравенство
выполняется неравенство
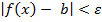 , обозначение:
, обозначение: 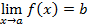 .
.
Определение 3. Функция 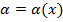 называется бесконечно малой при
называется бесконечно малой при 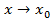 или и
или и 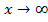 , если
, если
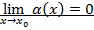 или
или 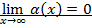
Свойства бесконечно малых величин.
1.Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию (постоянную, другую бесконечно малую величину) есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Определение 4. Функция 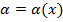 называется бесконечно большой при
называется бесконечно большой при 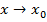 , если
, если 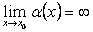 .
.
Свойства бесконечно больших величин.
1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Теорема. Связь между бесконечно малой величиной и бесконечно большой величиной. Если функция 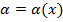 бесконечно малая при
бесконечно малая при 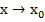 (
( 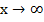 ), то функция f(x)=
), то функция f(x)= 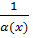 является бесконечно большой величиной при
является бесконечно большой величиной при 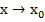 (
( 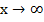 ). И, обратно, если функция
). И, обратно, если функция 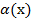 бесконечно большая при
бесконечно большая при 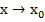 (
( 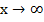 ),, то функция f(x)=
),, то функция f(x)= 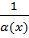 является бесконечно малой величиной при
является бесконечно малой величиной при 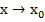 , (
, ( 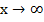 ).
).
Теоремы о пределах.
1. Функция не может иметь более одного предела.
2. Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций:
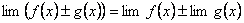 .
.
3. Предел произведения нескольких функций равен произведению пределов этих функций:
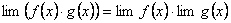
4. Предел степени равен степени предела: 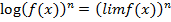
5. Предел частного равен частному пределов, если предел делителя существует:
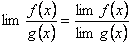 .
.
6. Первый замечательный предел.
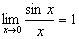 .
.
Следствия:
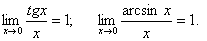
7. Второй замечательный предел:
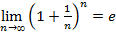 , n-натуральное число
, n-натуральное число
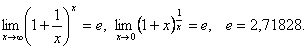
Следствия:
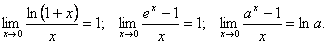
Эквивалентные бесконечно малые величины при 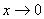 :
:
Техника вычисления пределов
При вычислении пределов используют основные теоремы о пределах, свойства непрерывных функций и правила, вытекающие из этих теорем и свойств.
Правило 1. Чтобы найти предел в точке 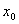 функции, непрерывной в этой точке, надо в функцию, стоящую под знаком предела, вместо аргумента x подставить его предельное значение
функции, непрерывной в этой точке, надо в функцию, стоящую под знаком предела, вместо аргумента x подставить его предельное значение 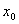 .
.
Пример 2. Найти 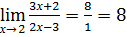
Правило 2. Если при отыскании предела дроби предел знаменателя равен нулю, а предел числителя отличен от нуля, то предел такой функции равен 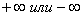 .
.
Пример 3. Найти 
Правило 3. Если при отыскании предела дроби предел знаменателя равен 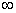 , а предел числителя отличен от нуля, то предел такой функции равен нулю.
, а предел числителя отличен от нуля, то предел такой функции равен нулю.
Пример 4. Найти 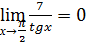
Часто подстановка предельного значения аргумента приводит к неопределенным выражениям вида
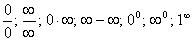 .
.
Нахождение предела функции в этих случаях называется раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразование данного выражения. Для раскрытия неопределенностей используют различные приемы.
Правило 4. Неопределенность вида 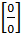 раскрывается путем преобразования подпредельной функции т.о., чтобы в числителе и знаменателе выделить множитель, предел которого равен нулю, и, сократив на него дробь, найти предел частного. Для этого числитель и знаменатель либо раскладывают на множители, либо домножают на сопряженные числителю и знаменателю выражения.
раскрывается путем преобразования подпредельной функции т.о., чтобы в числителе и знаменателе выделить множитель, предел которого равен нулю, и, сократив на него дробь, найти предел частного. Для этого числитель и знаменатель либо раскладывают на множители, либо домножают на сопряженные числителю и знаменателю выражения.
Пример 5.
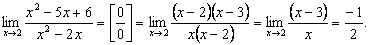
Пример 6
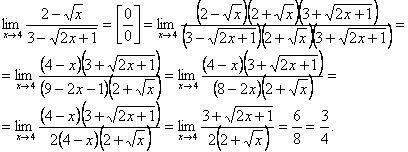
Правило 5. Если подпредельное выражение содержит тригонометрические функции, тогда, чтобы раскрыть неопределенность вида 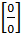 используют первый замечательный предел.
используют первый замечательный предел.
Пример 7.
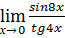 =2
=2 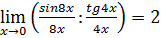 .
.
Пример 8.
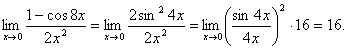
Правило 6. Чтобы раскрыть неопределенность вида  при
при  , числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.
, числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.
Возможны результаты:
1) искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если эти степени одинаковы;
2) предел равен бесконечности, если степень аргумента числителя выше степени аргумента знаменателя;
3) предел равен нулю, если степень аргумента числителя ниже степени аргумента знаменателя.
Пример 9.
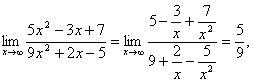
а) Степени равны, значит, предел равен отношению коэффициентов при старших степенях, т.е. 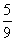 .
.
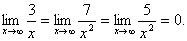
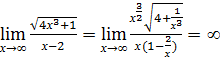
б) Степень числителя  , знаменателя – 1, значит, предел равен
, знаменателя – 1, значит, предел равен 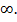
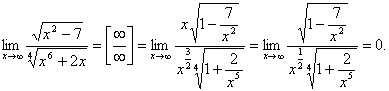
в) здесь степень числителя 1, а знаменателя -  , значит предел равен 0.
, значит предел равен 0.
Правило 7. Чтобы раскрыть неопределенность вида 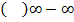 , числитель и знаменатель под предельной дроби необходимо умножить на сопряженное выражение.
, числитель и знаменатель под предельной дроби необходимо умножить на сопряженное выражение.
Пример 10.
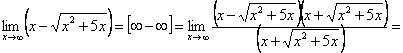
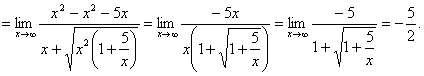
Правило 8. Чтобы раскрыть неопределенность вида 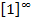 используют второй замечательный предел и его следствия.
используют второй замечательный предел и его следствия.
Можно доказать, что
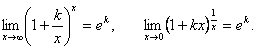
Пример 11.
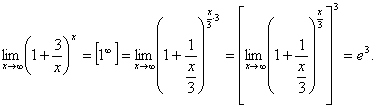
Пример 12.
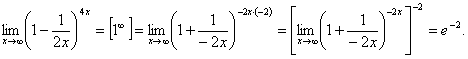
Пример 13.
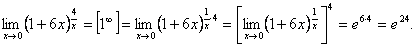
Правило 9. При раскрытии неопределенностей, подпредельная функция которых содержит бесконечно малые величины, необходимо заменить пределы этих бесконечно малых на пределы бесконечно малые, эквивалентных им.
Пример 14.
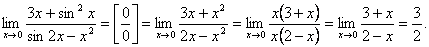
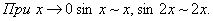
Пример 15.
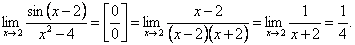
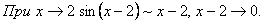
Некоторые замечательные пределы.
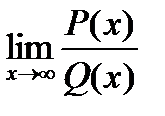 , где P(x) = a0xn + a1xn-1 +…+an,
, где P(x) = a0xn + a1xn-1 +…+an,
Q(x) = b0xm + b1xm-1 +…+bm - многочлены.
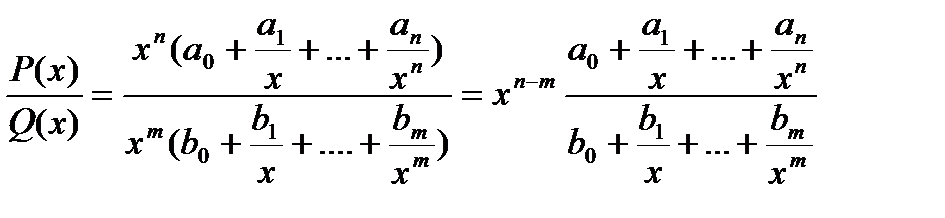
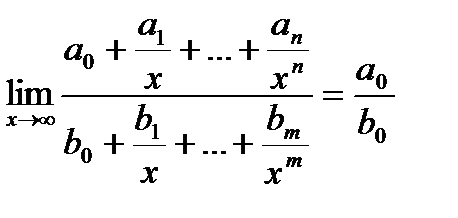
Итого: 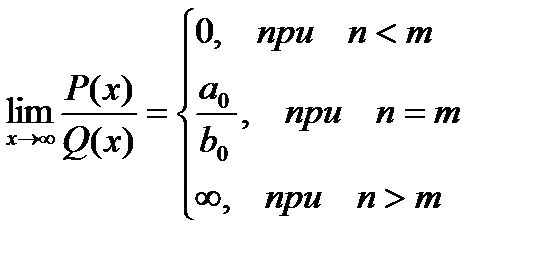
Первый замечательный предел. 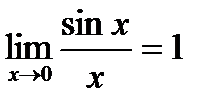
Второй замечательный предел. 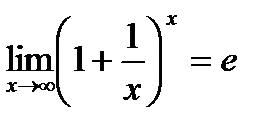
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
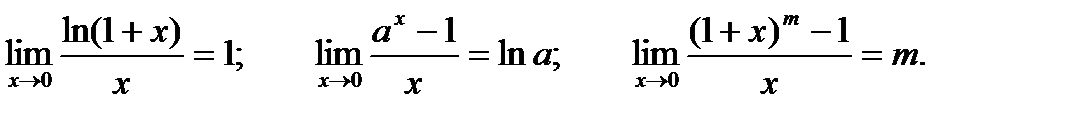
Пример. Найти предел.
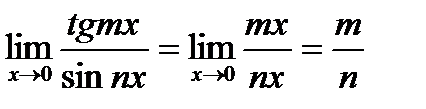
Пример. Найти предел.
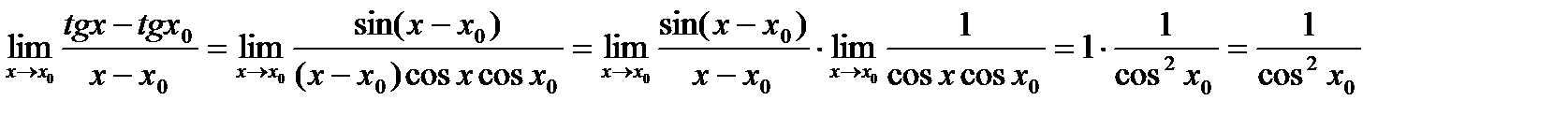 Пример. Найти предел.
Пример. Найти предел.
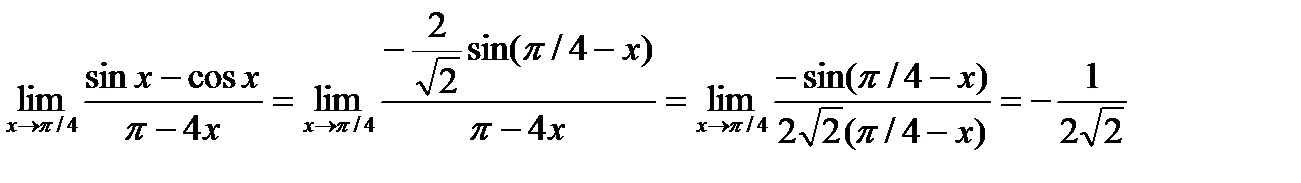
Пример. Найти предел.
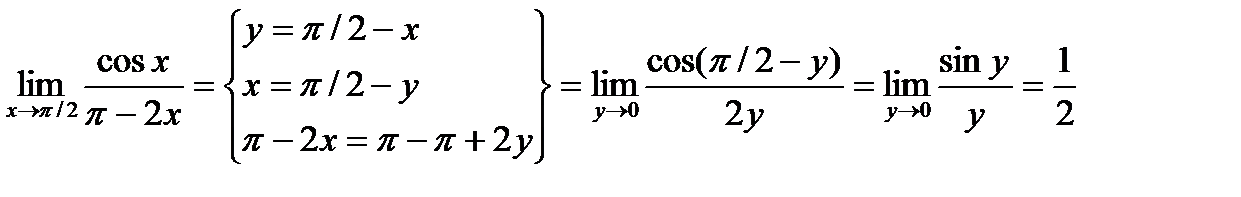
Пример. Найти предел.
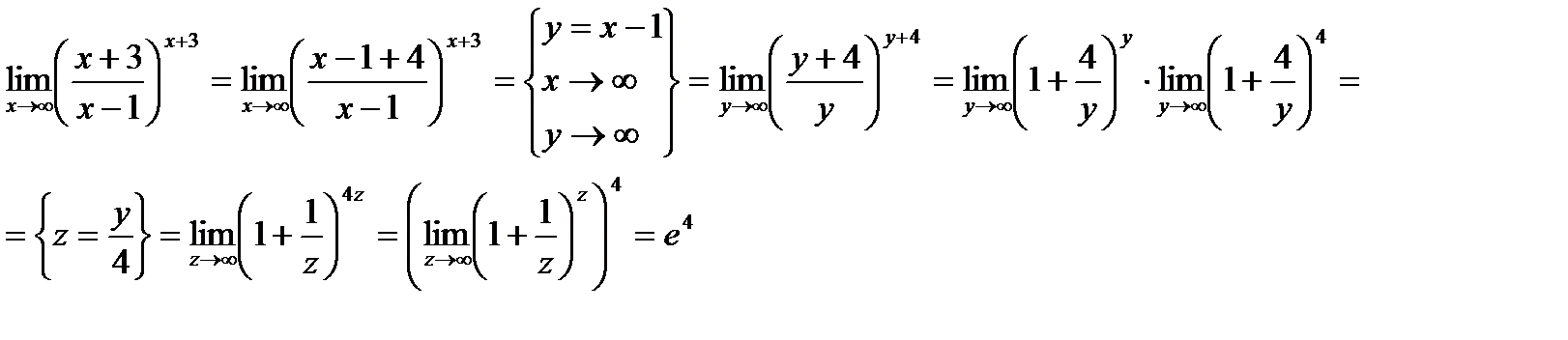
Пример. Найти предел 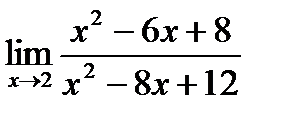 .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
x2 – 6x + 8 = 0; x2 – 8x + 12 = 0;
D = 36 – 32 = 4;D = 64 – 48 = 16;
x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6;
x2 = (6 – 2)/2 = 2 ; x2 = (8 – 4)/2 = 2;
Тогда 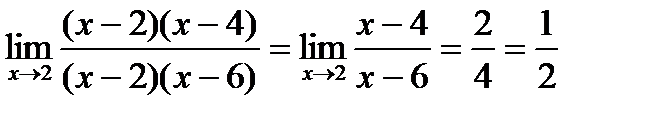
Пример. Найти предел.
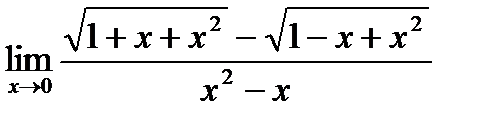 умножим числитель и знаменатель дроби на сопряженное выражение, т.е. на выражение
умножим числитель и знаменатель дроби на сопряженное выражение, т.е. на выражение 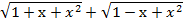 , получим:
, получим:
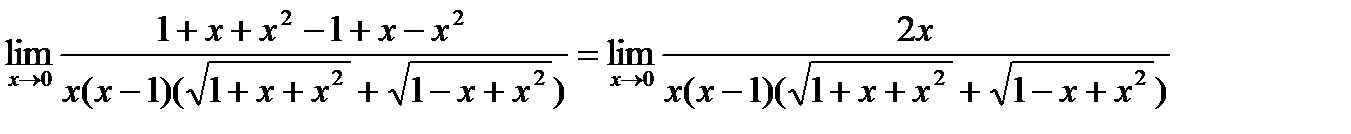 =
= 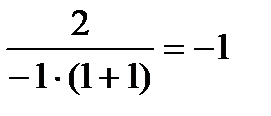 .
.
Пример. Найти предел.
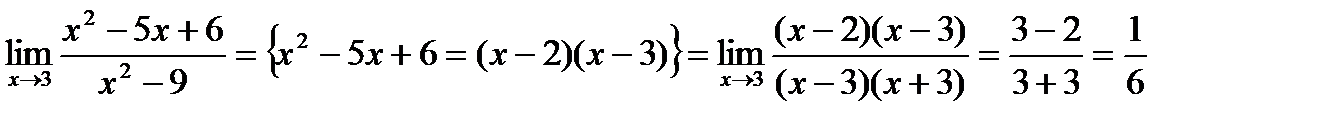
Пример. Найти предел 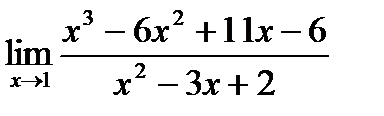 .
.
Если подставим в функцию вместо х значение (х=1), то получим неопределённость типа 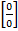 Разложим числитель и знаменатель на множители. Для этого разделим числитель на величину
Разложим числитель и знаменатель на множители. Для этого разделим числитель на величину
(х-1), получим квадратный трёх член x2 – 5x + 6, который решим стандартным способом через дискриминант, получим множители (x – 2)(x – 3). Знаменатель также легко представим в виде множителей (x – 2)(x – 3). Тогда можно записать:
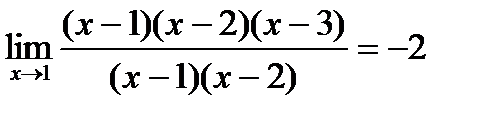
Пример. Найти предел.
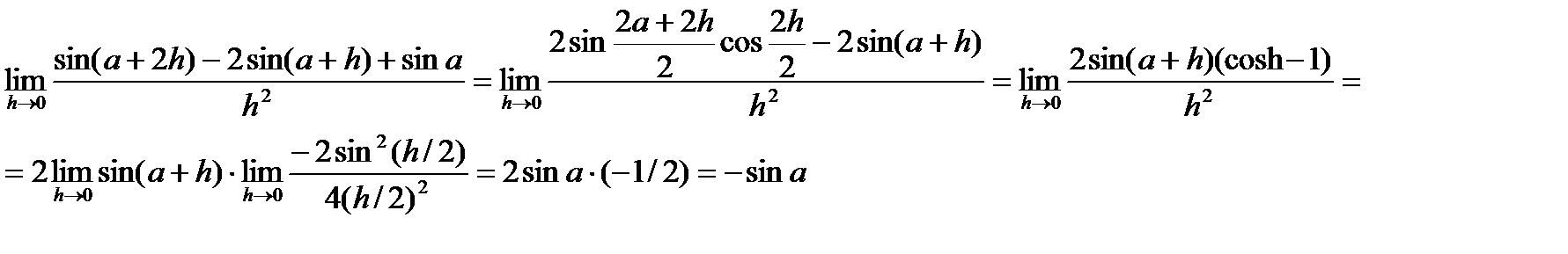
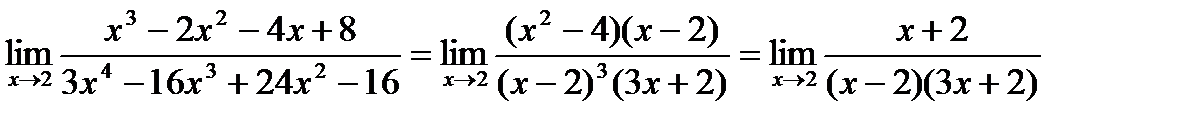 - не определен, т.к. при стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.
- не определен, т.к. при стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.
Дата добавления: 2016-06-05; просмотров: 4712;

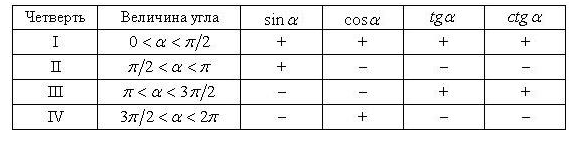 Некоторые значения тригонометрических функций
Некоторые значения тригонометрических функций
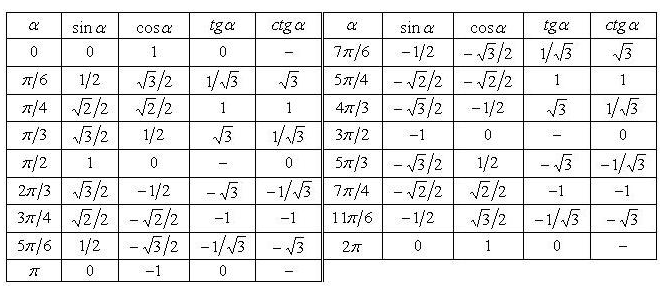 Логарифмические формулы
Логарифмические формулы