Элементарное уравнение кинетики (без учета запаздывающих нейтронов). Период реактора. Запаздывающие нейтроны

Ядра-осколки-родоначальники (ядра-предшественники) в силу пересыщенности нейтронами радиоактивны и с определенными периодами полураспада (β-распад) дают ядра-излучатели, непосредственно испускающие ЗН.

Из появляющихся более 600 осколков только 13 осколков (6 групп) характеризуются значительным суммарным выходом (>98%) и рабочим периодом полураспада (10^-6<Т_1/2<10³ c), например,

Суммарная доля выхода запаздывающих нейтронов всех 6 групп является нейтронно-физической константой делящихся ядер.

• для ядер 235U β5 = 0.0064,

• для ядер 239Pu β9 = 0.0021,

• для ядер 233U β3 = 0.0026

β - это среднее число запаздывающих нейтронов, приходящееся на один получаемый нейтрон деления в критическом реакторе бесконечных размеров.

Величина эффективной доли выхода ЗНb_эф для такого топлива должна находиться как средневзвешенное значение эффективных долей выхода ЗН для урана и плутония:

b_эф =(1- у) b_{эф 5} + у b_{эф 9} = c [0.0064(1- у) + 0.0021 у)],

где величина у = N₉ /( N₅ + N₉ ) - доля ядер Pu-239 от суммарного количества ядер U-235 и Pu-239 в топливе.

Так как в процессе кампании концентрация U-235 вследствие его выгорания уменьшается, а концентрация воспроизводимого Pu-239 растёт, то оказывается, что величина эффективной доли выхода запаздывающих нейтронов в процессе кампании однозначно уменьшается.

Средне время жизни поколения мгновенных нейтронов (lifetime – «l»):

l_мгн = t_дел + t_зам + t_диф ≈ 10^-13+10^-5+10^-4 с ≈ 10^-3-10^-5 с.

Встречаются около 60 типов осколков деления. Они появляются в свободном состоянии значительно позже мгновенных нейтронов и названы запаздывающими нейтронами. Характеризуется своей величиной удельного выхода (γi) и постоянной β−распада.

Время жизни ЗН больше на время их запаздывания:

l_ЗНi ≈ l_мгн + t_ЗНi.

Доля выхода ЗН i-ой группы: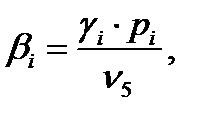

где ν₅=2.416 среднее число нейтронов деления, рождающихся в одном акте деления ядра ²³⁵U под действием ТН (всех – и МГН, и ЗН);

γ_i – удельный выход i-ой группы;

p_i – вероятность того, что осколок-родоначальник i-ой группы первым актом своей радиоактивной трансформации будет иметь β-распад.

Доля всех ЗН:

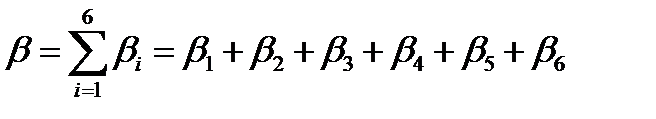
Среднее время жизни поколения с учетом ЗН (lifetime – «l»)

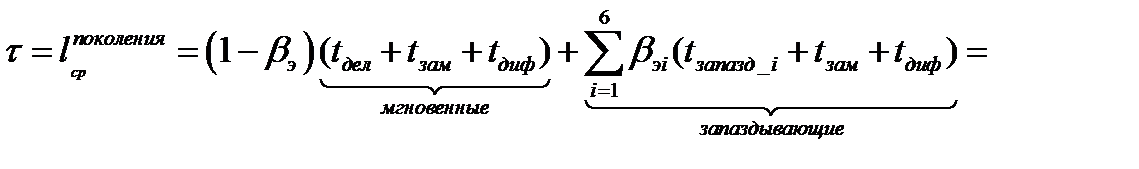
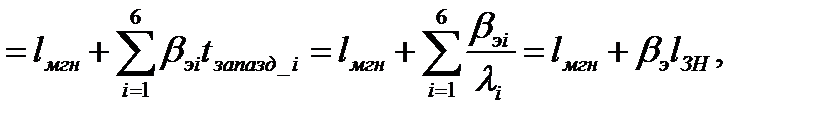
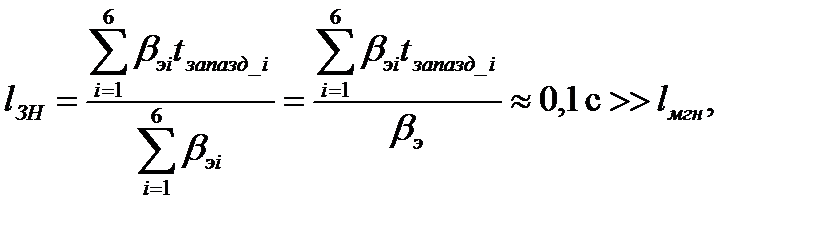
Где t _{запазд_i} = 1/ λ_i- среднее время запаздывания ЗН – это среднее время жизни испытывающих β-распад ядер-предшественников i-той группы (10^-2-10³ с) – величина, обратная постоянной β-распада ядер-предшественников для ЗН i-той группы;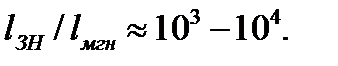

ЗН увеличивают время жизни поколения в целом в ≈10³ раз, делая переходные процессы в ЯР при изменении реактивности растянутыми во времени, а ЯР управляемым!

Уравнение элементарной кинетики (без учета ЗН)

Увеличение числа нейтронов за время одного цикла: δk = kэ-1

Если в 1 см3 n нейтронов, то: ∆n=n∙(kэ-1)=n∙ δk

Скорость изменения плотности тепловых нейтронов во времени за среднее время жизни поколения нейтронов l:

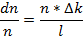
Элементарное уравнение кинетики реактора (ЭУКР) - дифференциальное уравнение с разделяющимися переменными:

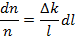
При начальных условиях: t = 0 n(0) = n0 - его решение является законом нейтронной плотности:

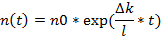
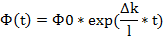
Характер зависимости n(t) определяется избыточной реактивностью k–1=Δk:

• При Δk=0 число нейтронов со временем не изменяется и ЦР не развивается, ЯР на данном уровне мощности критичен, так как условие критичности ЯР не определяется числом нейтронов в а.з. Все параметры ЯР (размер а.з., масса и пр.) при этом называются критическими.

• При Δk<0 число нейтронов со временем уменьшается, и такой ЯР называют подкритическим.

• При Δk>0 число нейтронов с течением времени растет, и такой ЯР называют надкритическим. Характерное время разгона реактора

Величина l / δkэ=Т, обратная величине показателя экспоненциала в решении элементарного уравнения кинетики реактора

n(t)=n_oexp(δk_эt / l),

· называется периодом реактора при заданной величине реактивности.

Решение элементарного уравнения кинетики реактора с учётом принятого обозначения периода имеет вид:

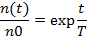
За время t = T величина плотности нейтронов в реакторе изменяется в е=2.718281... раз (при определённой постоянной величине сообщённой реактору реактивности, или при постоянной величине избыточного коэффициента размножения δkэ). Период реактора позволяет оценивать интенсивность изменения плотности нейтронов или мощность реактора, и при этом является легко воспринимаемой и легко измеряемой величиной.