Кинетика точечного реактора при линейном изменении реактивности
В процессе пуска ЯР и в процессе его перехода с одного уровня мощности на другой изменение реактивности происходит не скачком, а плавно, т.е. r≈Dk является функцией времени, на практике часто линейной:
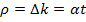
Рассмотрим ЯР с сосредоточенными параметрами (“точечный” ЯР) с учетом одной группы ЗН
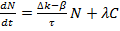 (3)
(3)
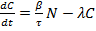 (4)
(4)
Записанную систему уравнений легко свести к уравнению второго порядка. Для этого сложим исходные уравнения (3)+(4):
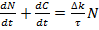 (5)
(5)
а уравнение (3) продифференцируем по времени:
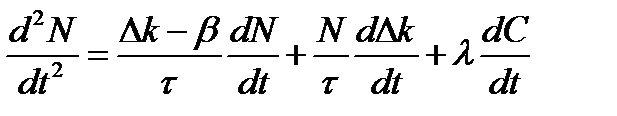 (6)
(6)
Для исключения dC/dt умножим уравнение (5) на λ и сложим с уравнением (6):
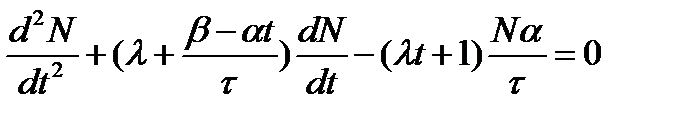 (7)
(7)
Нулевые условия имеют вид: t=0, N=N0, dN/dt=0. Последнее условие следует из того, что до переходного процесса ЯР считаем критическим и dC/dt = 0.
Отсюда из (4) (b/t)*N0=l*C0, Dk(0)=0 и из (3) следует, что (dN/dt)0=0. Решение уравнения (7) находится методом вариации произвольной постоянной.
Приведем качественный анализ уравнения (5). Если бы отсутствовало слагаемое с dN/dt, то уравнение имело бы вид:
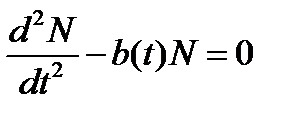
Решением такого уравнения, как известно, является экспонента. По аналогии с уравнением затухающих колебаний:
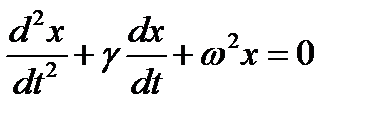 ,
,
наличие в уравнении (5) слагаемого, содержащего dN/dt, играет роль тормозящей силы, если это слагаемое входит в уравнение с положительным знаком. Решение уравнения (5) будет близко к экспоненциальному:
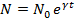
Дата добавления: 2021-05-28; просмотров: 689;











