Уравнение Нордхейма (обратных часов) и его решение

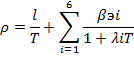
- уравнение обратных часов (УОЧ) или уравнение Нордхейма. Первое слагаемое определяет влияние мгновенных нейтронов, второе – запаздывающих.

Уравнение обратных часов имеет семь корней, тогда общее решение системы дифференциальных уравнений кинетики реактора будет не одной экспонентой, а будет представлять собой сумму семи экспонент, показатели которых определяются величинами этих семи корней уравнения обратных часов:

n(t) = A_oexp(t/T_o) + A₁exp(t/T₁) + A₂exp(t/T₂) + A₃exp(t/T₃) + A₄exp(t/T₄) + A₅exp(t/T₅) + A₆exp(t/T₆)

или в краткой форме:

,

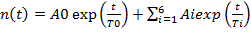где Т_о, T₁, T₂, ... , T₆ - значения семи корней уравнения обратных часов, а A_o, A₁, A₂, ... , A₆ - величины постоянных интегрирования, находимые путём подстановки в общее решение конкретных начальных условий.
Знаки корней уравнения обратных часов наиболее наглядно видны, если показать его решение в графическом виде:

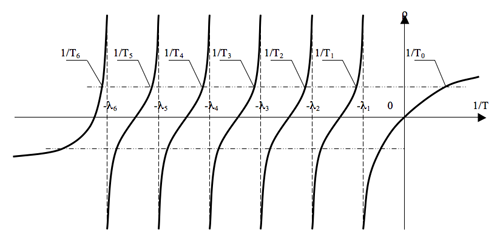
Рис. График зависимости корней уравнения обратных часов при положительных и отрицательных реактивностях разной величины.

На этом графике показано решение уравнения обратных часов в зависимости не от величины самого периода Т, а от обратной ему величины 1/Т: так удобнее выполнять решение уравнения аналитически.
Как видим, функция ρ = f (1/T) имеет шесть точек разрыва (второго рода), и именно благодаря этой разрывности отдельные корни уравнения обратных часов отображаются на графике достаточно наглядно: области изменения каждого из семи корней по оси 1/T лежат между соответствующими точками разрыва; например, нулевой обратный корень 1/Т_о лежит правее первой точки разрыва (- λ₁), первый обратный корень 1/Т₁ - между первой и второй точками разрыва (-λ₁и-λ₂), второй обратный корень 1/T₂ - между второй и третьей точками разрыва (-λ₂и-λ₃ ) и так далее; значения последнего, седьмого, обратного корня 1/Т₇ - располагаются левее последней, шестой, точки разрыва (-λ₆).
При этом знаки всех семи корней уравнения обратных часов определяются самым наглядным образом: в точках пересечения соответствующих участков графика с горизонтальной прямой, отсекающей на оси ординат рассматриваемое значение реактивности ρ.
Из графика видно, что, если величина сообщаемой реактору реактивности положительна, то нулевой обратный корень 1/Т_о , а, значит, и сам корень Т_о, - положителен (т.к. располагается в правой полуплоскости, правее оси О - ρ). Остальные шесть корней (Т₁ ÷ Т₆) уравнения обратных часов - отрицательны (лежат в левой полуплоскости). Если же величина сообщаемой реактору реактивности отрицательна, то все семь корней уравнения обратных часов отрицательны (лежат в левой, отрицательной, полуплоскости).Что касается величин самих корней, то они, как следует из графика, определяются только величиной сообщаемой реактору реактивности ρ.
Теперь о знаках постоянных интегрирования (А_о ÷ А₆). Здесь не приводится полный (и очень громоздкий) аналитический вывод общего выражения для любой из постоянных интегрирования, которое имеет вид:

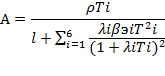
Квадрат выражения в скобках под знаком суммы, независимо от знака корня Т_i, всегда имеет положительный знак, и, поскольку все остальные величины знаменателя положительны, то весь знаменатель - всегда положителен. А раз так, то знак постоянной интегрирования А_i всегда определяется знаком произведения ρТ_i в числителе правой части этого выражения. То есть, если нулевой корень Т_о при ρ > 0, как говорилось выше, положителен (Т_о>0), то произведение ρТ_о > 0, а, следовательно, А_о > 0. При отрицательной же величине реактивности (ρ < 0) произведение отрицательного нулевого корня Т_о на отрицательную величину реактивности ρ даёт положительную величину произведения ρТ_о, и, следовательно, величина нулевой постоянной интегрирования будет иметь положительный знак. Проделав такой микроанализ со всеми величинами постоянных интегрирования, можно прийти к общему выводу:

·приρ>0: Т_о>0 и А_о>0, а остальные корни (Т₁÷Т₆)<0 и (А₁÷А₆)<0;

· приρ<0: все 7 корней (Т_о÷Т₆)<0, а постоянные интегрирования (А_о÷А₆)>0.