Эффекты и коэффициенты реактивности.
Для анализа и прогнозирования поведения реактора в переходных режимах удобнее разложить полный эффект реактивности на эффекты по отдельным факторам.
Эффект реактивности по фактору х — это изменение реактивности, возникающее в реакторе при изменении параметра х.
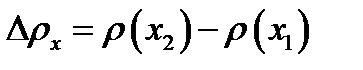
Эффекты реактивности зависят от типа реактора. В реакторах ВВЭР рассматривают температурный, барометрический, мощностной эффекты реактивности, эффект реактивности, связанный с изменением концентрации борной кислоты в воде. В реакторах РБМК наряду с температурным, мощностным эффектами реактивности измеряют паровой эффект реактивности, эффект реактивности по температуре замедлителя (графита), эффект обезвоживания контура охлаждения СУЗ.
Каждый из эффектов имеет свою специфику и влияние на безопасность работы реактора.
В свою очередь, каждый эффект реактивности удобно соотнести с единичным изменением соответствующего параметра. Тогда приходим к понятию "коэффициент реактивности".
Коэффициент реактивности (aх) – это величина отклонения реактивности (Dr) в ответ на единичное изменение соответствующего параметра (Dх).
Исходя из определения, коэффициент реактивности можно представить выражением:
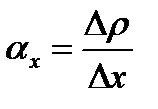
Коэффициент реактивности является производной от реактивности как функции параметра х. Графически коэффициент реактивности определяется касательной к кривой, описывающей зависимость реактивности 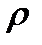 от параметра х.
от параметра х.
Если с увеличением параметра "х" вводится положительная реактивность, тогда aх считается положительным. Если с увеличением параметра "х" вводится отрицательная реактивность, тогда aх отрицателен.
Эффект реактивности можно рассчитать, умножив коэффициент реактивности на величину изменения параметра. В общем случае эффект реактивности определяется соотношением:
Dr = aхDх
6.2. Мощностной эффект реактивности. Эффект Доплера
В тех случаях, когда теплопроводность используемого в реакторе ядерного топлива мала (как, например, у UO2 в реакторах ВВЭР), с увеличением мощности весьма значительно возрастает радиальная неравномерность распределения температур в элементарной ячейке вследствие увеличения температуры в центре твэлов. В результате средне интегральная по объему активной зоны температура становится функцией мощности и средняя температура теплоносителя оказывается малоподходящим аргументом для характеристики температурного эффекта реактивности, так как при ее использовании предполагается незначительное изменение радиальной неравномерности температурного поля в ячейке. Поэтому применяются также характеристики мощностного эффекта реактивности, используемые при работе реактора в энергетических режимах. При этом различают мощностной эффект и мощностной коэффициент реактивности.
Мощностным эффектом реактивности реактора на данном уровне его мощности (Np) называют величину изменения реактивности, возникающего в разогретом до номинальной средней температуры теплоносителя реакторе вследствие подъёма его тепловой мощности от 0 (от МКУМ) до данного уровня Np.
Мощностным коэффициентом реактивности реактора на данном уровне его тепловой мощности называется изменение реактивности в разогретом до номинальной средней температуры теплоносителя реакторе при подъёме его тепловой мощности на 1 МВт сверх данного уровня.
МЭР и МКР обозначаются соответственно 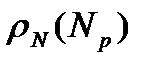 и
и 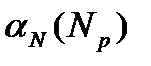 и измеряются соответственно в % и %/МВт. Они (как и ТЭР с ТКР) представляют собой интегральную и дифференциальную меры влияния мощности реактора на его реактивность и взаимосвязаны аналогичными зависимостями:
и измеряются соответственно в % и %/МВт. Они (как и ТЭР с ТКР) представляют собой интегральную и дифференциальную меры влияния мощности реактора на его реактивность и взаимосвязаны аналогичными зависимостями:
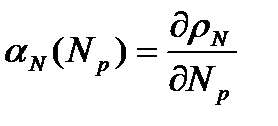 и
и 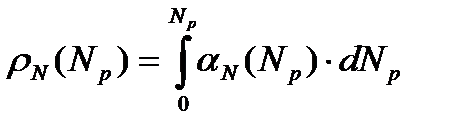 .
.
Хотя мощностной эффект (и коэффициент) реактивности имеют своё название и обозначение, не будем забывать, что их происхождение – температурное. По существу, это – определяемая температурой топлива доплеровская составляющая температурного изменения реактивности, но поставленная в соответствие не температуре топлива, а другому аргументу – тепловой мощности реактора. При неизменной средней номинальной температуре теплоносителя изменение мощности приводит к изменению средней температуры топливной композиции. Последнее воздействует на размножающие свойства реактора, главным образом, через доплеровское изменение величины j (вероятности избежание резонансного захвата замедляющихся нейтронов). Изменение с температурой топлива величины коэффициента использования тепловых нейтронов хотя и имеет место, но оно меньше Доплер-эффекта примерно на два порядка величины, поскольку оно определяется не столько температурой топлива, сколько температурой нейтронов, которая, в свою очередь, зависит не столько от температуры топлива, сколько от средней температуры замедлителя-теплоносителя в ВВЭР. Вот почему мощностное температурное изменение реактивности реактора часто называют доплеровским.
И ещё об одном распространённом названии. МЭР (МКР) определяются самой динамично изменяющейся температурой в реакторе – температурой топлива, и мощностное изменение реактивности в реакторе происходит безынерционно, практически отслеживая без запаздывания величину мощности и величину средней температуры топлива. Поэтому МКР часто называют быстрым мощностным коэффициентом реактивности. Это делается в тех случаях, когда требуется отличить чисто мощностное изменение реактивности от полного изменения реактивности, вызываемого изменением мощности реактора и дополняемого (с некоторым запаздыванием) изменением реактивности, обусловленным изменением средней температуры теплоносителя.
Расчёт мощностных изменений реактивности реактора производится по стереотипной формуле:
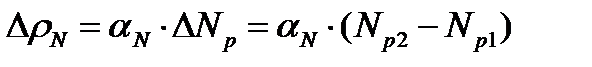 ,
,
в которую величины мощности подставляются в МВт, а величина МКР извлекается из располагаемой оператором рабочей документации.
При этом следует иметь в виду, что МКР – величина не постоянная, а зависящая от уровня мощности реактора, поэтому в данной формуле подставляется среднее в интервале изменения мощности значение МКР. Это значение находится следующим образом.
Оператор из рабочей документации (из графиков или таблиц) может без особых затруднений извлечь достоверное на данный момент кампании значение МКР на номинальном (100%-ном) уровне мощности реактора - 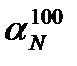 . На нулевом уровне мощности величина МКР меньше указанной величины, но она не равна нулю, а составляет приблизительно третью часть от величины МКР на полной мощности реактора. Полагая, что в интервале от 0 до номинальной мощности текущее значение aNвозрастает по линейному закону (а это практически так и есть), величина МКР на исходном уровне мощности (Np1) найдётся как
. На нулевом уровне мощности величина МКР меньше указанной величины, но она не равна нулю, а составляет приблизительно третью часть от величины МКР на полной мощности реактора. Полагая, что в интервале от 0 до номинальной мощности текущее значение aNвозрастает по линейному закону (а это практически так и есть), величина МКР на исходном уровне мощности (Np1) найдётся как
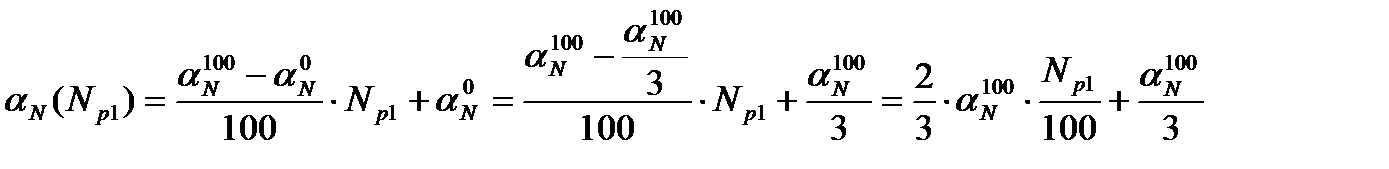 .
.
Аналогично величина МКР на конечном уровне мощности Np2: 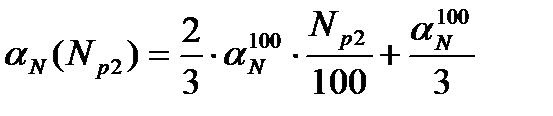 , и поэтому среднее значение МКР в интервале изменения мощности (Np1, Np2):
, и поэтому среднее значение МКР в интервале изменения мощности (Np1, Np2): 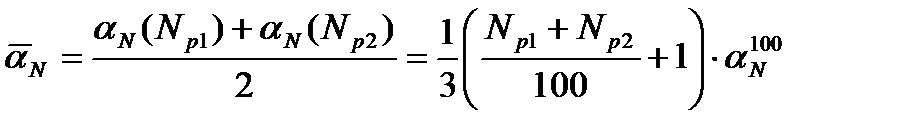 .
.
Таким образом, для того, чтобы рассчитать изменение реактивности за счёт изменения уровня мощности реактора от Np1 до Np2 в данный момент кампании, для расчёта среднего значения МКР требуется извлечь из рабочей документации только достоверное на этот момент кампании значение МКР на номинальной мощности реактора. Удобнее всего для этой цели пользоваться имеющимся в распоряжении оператора рассчитанным графиком, качественный вид которого показан на рис.6.3.
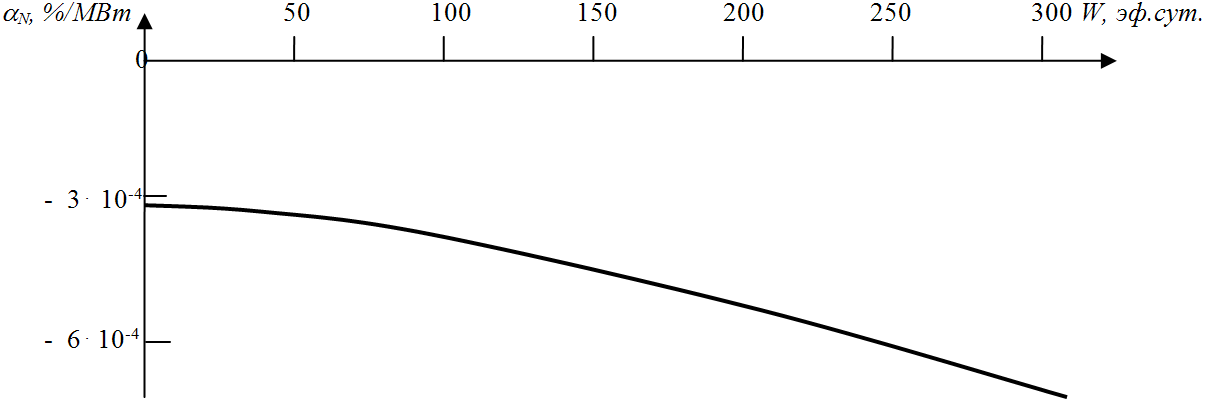
Рисунок 6.3.Величина МКР реактора на номинальной мощности в различные моменты кампании.
Из сказанного эксплуатационнику полезно взять на заметку следующее.
1. С точки зрения устойчивости работы реактора на мощности сказанное ранее об условии обеспечения этой устойчивости полностью касается и МКР: в разогретом до номинальной температуры реакторе мощностной коэффициент реактивности должен быть обязательно отрицательным.
2. Абсолютная величина МКР на малых уровнях мощности реактора всегда меньше, чем на больших мощностях. Это значит, что с ростом мощности реактора его устойчивость растёт. И опасаться недостаточно устойчивой работы реактора следует именно на МКУМ и малых уровнях мощности.
3. В процессе кампании величина отрицательного МКР реактора монотонно увеличивается. Следовательно, снижения устойчивости реактора в процессе кампании можно не опасаться.
Зависимость мощностного эффекта от расхода проявляется лишь в том, что с увеличением расхода мощностной эффект уменьшается, так как при этом улучшается теплосъем и снижается температура ядерного топлива. Данный процесс в общем случае показан на рисунке 6.3.
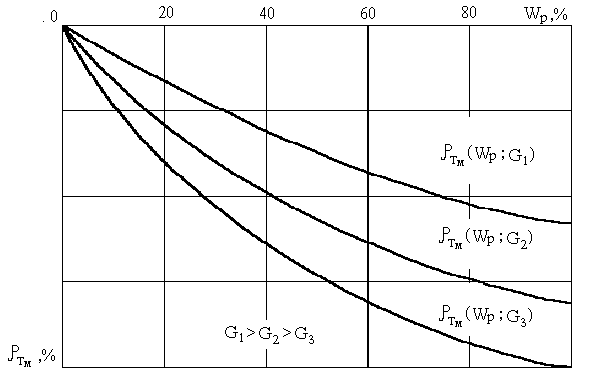
Рис. 6.4 Общий вид кривых мощностного эффекта реактивности
Для каждого реактора, строятся свои кривые мощностного эффекта реактивности (смотри рисунок 6.4).
Следует иметь в виду, что мощностной коэффициент реактивности в неустановившемся процессе может существенно отличатся от своего стационарного значения при том же мгновенном значении мощности реактора. Отличие это тем больше, чем больше скорость переходного процесса.
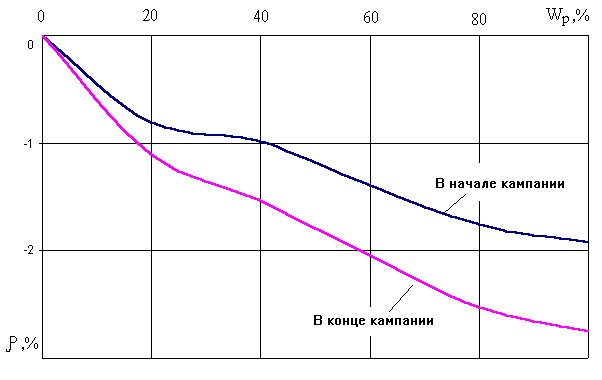
Рис. 6.5 Кривые мощностного эффекта реактивности в начале и в конце кампании (блок №4, 9 кампания)
6.3. Температурный эффект и температурный коэффициент реактивности
6.1.1. Основные понятия
В энергетических реакторах материалы находятся при столь высоких температурах (например, в ВВЭР средняя температура топливаtuo2≥1000 °C, а водыth2o=300 °C), что даже относительно малые отклонения от номинальных режимов работы приводят к значительным абсолютным изменениям температур. Особенно велики эти изменения при переходных режимах работы реакторов. Увеличение температуры приводит к расширению материалов, из-за чего изменяются соотношения между массовыми и объемными долями компонентов реактора и увеличиваются размеры активной зоны и реактора в целом. Кроме того, при этом повышаются скорости движения атомов и существенно уширяются резонансы в зависимостях сечения поглощения от энергии для тяжелых ядер. Все эти температурные эффекты вызывают изменение эффективного коэффициента размножения (или реактивности).
Распределение температуры по объему реактора, вообще говоря, изменяется во времени. Однако для многих практических задач с достаточной степенью точности можно считать, что в любой момент времени справедливо установившееся поле температур (квазистационарное приближение). Тогда в задаче о влиянии температуры материалов на реактивность можно рассматривать средние по объему отдельных компонентов реактора температуры, а не истинные распределения. Такой подход обычно применяется для описания медленных переходных режимов реактора.
Иногда реактор рассматривается как единое целое, описываемое средней температурой. Этот простейший подход к рассмотрению температурных эффектов наиболее удобен для качественного выяснения зависимости kэф (или ρ) от температуры. Принято вводить понятия температурного эффекта и температурного коэффициента реактивности Температурным эффектом реактивности Δρt называется изменение реактивности ρ, вызванное изменением температуры всех материалов реактора от значения t1 до значения t2
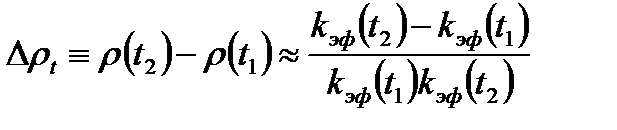
Температурный коэффициент реактивности определяется как приращение реактивности, соответствующее изменению температуры всех материалов реактора на 1°С, т.е.
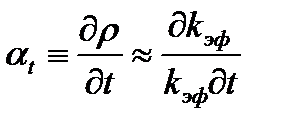
Величины Δρt и αt называют изотермическими Реальные значения Δρt и αtмогут изменяться при переходе как от одного реактора к другому, так и от одного интервала температур к другому (для конкретного реактора), поскольку в общем случае Δαt=f(t). Зная зависимость температурного коэффициента реактивности от температуры, легко оценить температурный эффект реактивности, связанный с изменением температуры реактора от t1 до t2
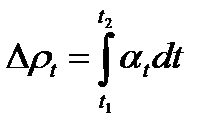
В случае квазистационарного приближения принято говорить о температурных коэффициентах реактивности по топливу, замедлителю, теплоносителю или отражателю, и в определениях использовать температуру t, относящуюся к рассматриваемому эффекту (соответственно средняя температура топлива, замедлителя, теплоносителя, либо отражателя). Для определения соответствующего температурного эффекта реактивности можно использовать результаты расчетов kэф при требуемых температурах. Такой подход позволяет рассчитать любой температурный эффект реактивности, в том числе и соответствующий различным изменениям средних температур всех компонентов реактора.
Для выяснения степени влияния отдельных температурных эффектов на температурный коэффициент реактивности αt удобно представить kэф в виде произведения k∞P. Тогда
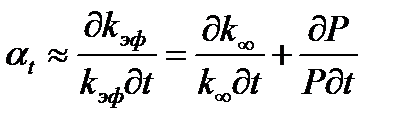 или
или 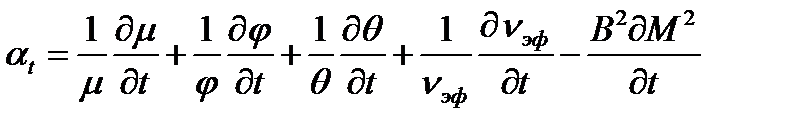
Таким образом, задача сводится к выяснению зависимостей μ, φ, θ, νэф, М2 и В2 от температуры t.
Изменение данных параметров, обусловленно главным образом двумя факторами:
· изменением макроскопических сечений взаимодействия нейтронов с ядрами атомов, скорость которых увеличивается по мере разогрева размножающей среды;
· изменением плотности материалов активной зоны, определяющей их концентрацию, а следовательно, и макроскопические сечения.
В целях раздельного учета названных факторов при анализе зависимостей ТЭР и ТКР от температуры ТКР ВВЭР условно разделяют на две составляющие: ядерный ТЭР rя, определяющий зависимость реактивности от микроскопических сечений материалов активной зоны при условии постоянства их плотностей; и плотностной ТЭР rп, определяющий зависимость реактивности от плотности материалов активной зоны при условии постоянства их микроскопических сечений.
Очевидно, при известныхrяи rплегко определить полный температурный эффект реактивности: rт = rя + rп. Аналогичным образом можно записать: aт = aя +aп. Проанализируем каждую из составляющих ТЭР и ТКР.
6.1.2. Ядерный температурный эффект реактивности
Общая характеристика составляющих ядерного ТЭР. Для удобства анализа целесообразно разделить ядерный ТЭР на две составляющие:
- обусловленную изменением температуры замедлителя и приводящую к изменению жесткости спектра тепловых нейтронов;
- обусловленную изменением температуры топлива и приводящую к уширению резонансов, в зависимости сечения поглощения от энергии нейтроном (так называемый эффект Доплера).
Первая составляющая связана с изменением энергии нейтронов, находящихся в тепловом равновесии с размножающей средой. Увеличение температуры среды (основное значение имеет температура замедлителя) приводит к смещению спектра тепловых нейтронов в сторону более высоких энергий. Поскольку сечения поглощения снижаются с ростом энергии нейтронов, разогрев уменьшает поглощение нейтронов в активной зоне реактора. Кроме того, вследствие увеличения энергии сшивки с ростом температуры при разогреве сокращается интервал замедления нейтронов.
Вторая составляющая относится к промежуточной области энергий и не связана с распределением тепловых нейтронов по энергиям. Она определяется лишь изменением относительной скорости движения в системе нейтрон-ядро, которая увеличивается с ростом абсолютной скорости ядер при разогреве и уменьшается по мере снижения абсолютной скорости ядер при расхолаживании. Изменение температуры приводит к изменению резонансных пиков сечения поглощения ядер 238U, что связанно с изменением абсолютной скорости теплового движения ядер относительно абсолютной скорости движения нейтронов. Чем выше температура, тем больше понижение и уширение резонансного пика. При этом независимо от температуры площадь под кривой резонансного пика всегда остается неизменной. Изменение формы резонансов вследствие теплового движения ядер названо доплер-эффектом.
Доплер-эффект оказывает влияние только на вероятность избежать резонансного захвата, в то время как эффект смещения спектра тепловых нейтронов в той или иной степени сказывается на всех остальных характеристиках размножения. Так как доплеровское изменение ширины резонансных пиков является следствием изменения температуры топлива, а смещение спектра тепловых нейтронов вызывается изменением температуры замедлителя, то в динамическом отношении эти эффекты далеко не равнозначны.
Анализ составляющих ядерного ТКР. После общей характеристики составляющих ядерного ТЭР проанализируем с использованием выражения (7) зависимость от температуры слагаемых ядерного ТКР, определяющего в конечном счете ядерный ТЭР.
Начнем со слагаемого 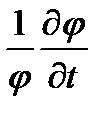 , характеризующего влияние температуры на вероятность избежать резонансного захвата.
, характеризующего влияние температуры на вероятность избежать резонансного захвата.
Удобно записать в виде: 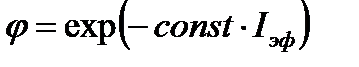 , так как влияние эффекта Доплера на вероятность для нейтронов избежать поглощения в процессе замедления сказывается только через эффективный резонансный интеграл Iэф. В гетерогенных реакторах j всегда зависит от температуры топлива и с ростом последней j уменьшается. В результате вклад резонансного захвата в ядерный ТКР оказывается отрицательным, т.е.:
, так как влияние эффекта Доплера на вероятность для нейтронов избежать поглощения в процессе замедления сказывается только через эффективный резонансный интеграл Iэф. В гетерогенных реакторах j всегда зависит от температуры топлива и с ростом последней j уменьшается. В результате вклад резонансного захвата в ядерный ТКР оказывается отрицательным, т.е.: 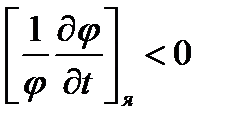 .
.
Физически указанная закономерность вполне очевидна. Увеличение температуры при прочих равных условиях приводит к снижению j, так как в этом случае за счет отличия энергии относительного движения нейтронов от их абсолютной энергии большее число нейтронов может попасть в область резонанса.
Можно считать, что 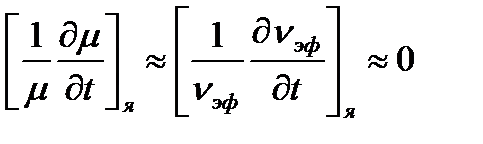 .
.
Величина m от энергии нейтронов зависит только в связи с изменением Р-вероятности первого соударения нейтрона в урановом блоке. Зависимость эта существует только при учете неравномерности распределения тепловых, а следовательно, и рождающихся нейтронов по блоку. При оценке температурного эффекта указанная зависимость столь незначительна, что ею с полным основанием можно пренебречь.
Величина nэф также мало изменяется с изменением температуры. Существующая слабая зависимость nэф(Тср) обусловлена тем, что микроскопические сечения sf5 и sа5 по-разному отклоняются от закона 1/v в случае изменения температуры размножающей среды.
Чтобы оценить вклад в aя слагаемого 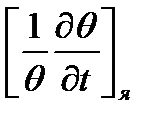 , необходимо обратиться к выражению: 1/Q = 1+ VзSазФзср/(VтSа5Фuср).
, необходимо обратиться к выражению: 1/Q = 1+ VзSазФзср/(VтSа5Фuср).
Из этого выражения следует, что коэффициент использования тепловых нейтронов при постоянной плотности компонентов размножающей среды обратно пропорционален произведению коэффициента проигрыша Фзср/ФUср на отношение sаз/sа5.
Коэффициент проигрыша определяется в результате суммирования внешнего и внутреннего блок-эффектов, характеризующих неравномерность распределения потока нейтроновв элементарной ячейке. Ввиду того что с повышением температуры среды поглощение нейтронов уменьшается, длина диффузии в материалах ячейки возрастает. Это приводит к уменьшению неравномерности распределения потока (Ф¢) в ячейке (рис. 6.6) и, следовательно, к снижению коэффициента проигрыша, что положительно сказывается на величине Q.
Отношение sаз/sа5, являющееся одним из параметров, которые характеризуют относительное поглощение нейтронов в замедлителе, претерпевает изменения вследствие того, что sаз с увеличением температуры уменьшается пропорционально 1/v, а sа5 изменяется с отклонением от закона 1/v. В результате этого при разогреве ядерные эффекты увеличивают относительное поглощение нейтронов в замедлителе, что отрицательно сказывается на величине Q.
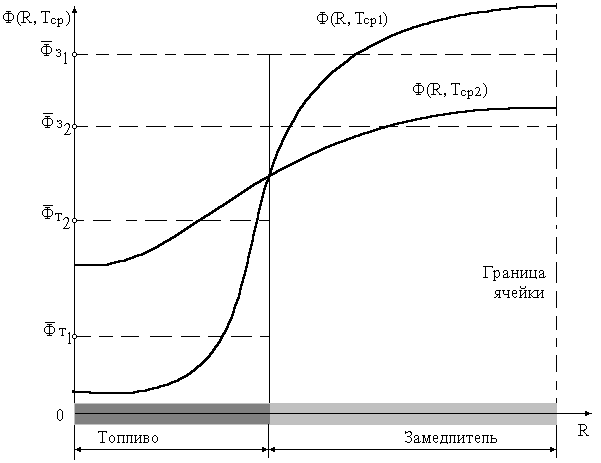
Рис.6.6 Характер изменения радиального распределения j в элементарной ячейке при увеличении средней температуры от Тср1 до Тср2
Поскольку рассмотренные факторы по-разному влияют на Q, результат будет зависеть от соотношения их вкладов. Проведенная оценка влияния указанных факторов на aя при разогреве реактора свидетельствует о том, что 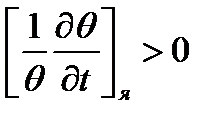 .
.
Температурная зависимость слагаемого 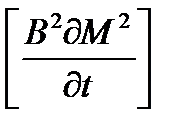 , где
, где 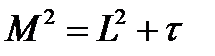 , также определяется в результате сопоставления двух конкурирующих эффектов, так как при увеличении Тср значениеL2 растет из-за снижения поглощения, а t уменьшается вследствие увеличения энергии сшивки и соответствующего сокращения интервала замедления. В результате
, также определяется в результате сопоставления двух конкурирующих эффектов, так как при увеличении Тср значениеL2 растет из-за снижения поглощения, а t уменьшается вследствие увеличения энергии сшивки и соответствующего сокращения интервала замедления. В результате 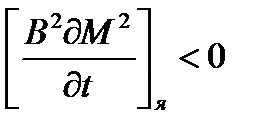 , что определяется величиной
, что определяется величиной 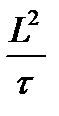 .
.
Подводя итог сказанному, можно заключить, что ядерный ТКР определяется следующим полученным на базе (7) равенством:
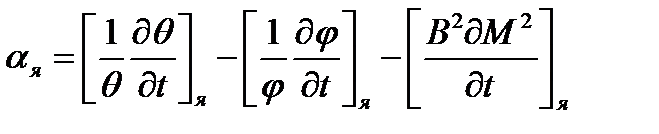
Во многом знак aя зависит от вида функции ТUср=f(Tср). В случае, когда изменение средней температуры топлива D ТUср примерно равно изменению средней температуры замедлителя D Тзср, первое слагаемое оказывается больше, чем второе. Эффект изменения j начнет превалировать над эффектом изменения Q только при (D ТUср/D Тзср)³3. Знак ТКР имеет важное значение, так как он в значительной степени влияет на устойчивость реактора, о чем будет сказано ниже, и определяет знак ядерного ТЭР.
В заключение следует отметить, что выше рассмотрены те эффекты, которые являются наиболее общими. Вообще же при анализе температурного коэффициента и температурного эффекта реактивности кроме рассмотренных необходимо учитывать и такие факторы:
- изменение эффективности отражателя, который через эффективную добавку влияет на геометрический параметр и, следовательно, на r;
- изменение эффективности средств регулирования мощности и компенсации реактивности, что влияет на Q и соответственно на r;
- изменение поглощения нейтронов накопившимися в активной зоне нуклидами с большим сечением поглощения (239Pu, 135Xe, 149Sm), что сказывается на Qи соответственно на r.
6.1.3. Плотностной температурный эффект реактивности
В соответствии с приведенным выше определением этот эффект характеризует зависимость rт=f(r) при s=const. Чтобы установить основные качественные закономерности, нужно, как и при рассмотрения ядерного эффекта, обратиться к равенству (12.4) и проанализировать, какое влияние на каждое слагаемое оказывает изменение плотности материалов активной зоны. А зная характер изменения ТКР, можно оценить и соответствующий ему плотностной температурный эффект.
Слагаемое выражения (12.4), содержащее nэф, от плотности не зависит, так какnэф = n5sf5/sа5. Следовательно, [1/nэф(dnэф/dT)]п=0.
Слагаемое содержащееm, с изменением плотности изменяется, так как m является функцией относительной концентрации водорода NH/N8. Поскольку с увеличением температуры относительная концентрация водорода уменьшается, то m увеличивается и вклад в температурный коэффициент реактивности получается положительным. Следовательно, [1/m(dm/dT)]п>0.
Слагаемое содержащее Q, претерпевает температурные изменения при s=const, потому что изменения температуры в ВВЭР ощутимо влияют только на плотность воды (остальные материалы практически не изменяют своей плотности). В результате изменяется уран-водное отношение VтNu/(VН2ОNН2О) в элементарной ячейке, что существенно сказывается на относительном поглощении нейтронов в замедлителе. Разогрев ведет к уменьшению плотности воды и, значит, NН2О, вследствие чего уран-водное отношение увеличивается. Поскольку при этом относительное поглощение в замедлителе уменьшается, то Q возрастает. Точно так же при расхолаживании вследствие уменьшения уран-водного отношения значение Q снижается. Указанная зависимостьQ от уран-водного отношения свидетельствует о том, что величина Q прямо пропорциональна Т.
Следовательно, [1/Q(dQ/dT)]п>0 и соответствующая составляющая температурного эффектаположительна.
Слагаемое, содержащее j,определяется температурной зависимостью y. Согласно (5.9) величинаy прямо пропорциональна уран-водному отношению, которое в свою очередь прямо пропорционально температуре. Так как j = exp(- y), то на основании сказанного можно заключить, что j обратно пропорциональна Т. Следовательно, [1/j(dj/dT)]п<0, и соответствующая составляющая температурного эффекта отрицательна.
Слагаемое, содержащее M2, весьма существенно зависит от плотности, поскольку и длина диффузии, и возраст обратно пропорциональны произведению макроскопических сечений. Если M2(Т1) - площадь миграции при температуре Т1, которой соответствует плотностьr(Т1), а M2(Т2) - площадь миграции при температуре Т2, которой соответствует плотностьr(Т2), то можно записать:
M2(Т2)/ M2(Т1) = r2(Т1)/ r2(Т2)
Так как площадь миграции изменяется обратно пропорционально квадрату плотности, то с увеличением температуры M2 возрастает, следовательно, [B2dM2/dT]п>0. Знак минус перед этим слагаемым в (7) означает, что с увеличением площади миграции вероятность избежать утечки нейтронов уменьшается, и это отрицательно сказывается на реактивности. В результате можно заключить, что зависящая от M2 составляющая плотностного температурного эффекта реактивности при увеличении Т будет отрицательной. Особенно велик эффект изменения M2 в ВВЭР, где и замедлитель, и теплоноситель существенно изменяют свою плотность при изменении температуры.
С учетом всего сказанного равенство (12.4) при выполнении условия s=const будет иметь вид:
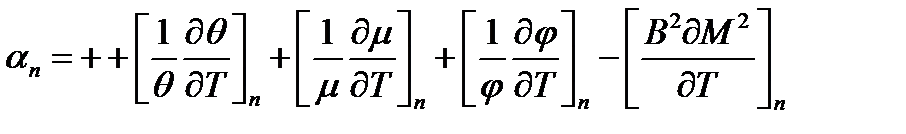
Знак и значение aп, а также зависимость aп=f(T) определяются соотношением вкладов слагаемых выражения (12.8). В ВВЭР обычно вклад aп суммарный температурный коэффициент реактивности оказывается существенно больше вклада aя и зависимость aп=f(T) часто определяет полную функцию a=f(T).
В заключение следует заметить, что плотностной эффект влияет на реактивность ВВЭР главным образом в период разогрева после пуска реактора и в процессе его расхолаживания, так как при работе реактора в энергетических режимах средняя температура обычно поддерживается постоянной на всех уровнях мощности.
6.4. Барометрический и паровой эффект реактивности
Дата добавления: 2021-05-28; просмотров: 3373;











