СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Определённый интеграл не зависит от обозначения переменной интегрирования:
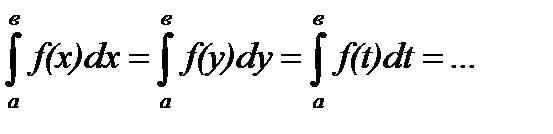 ;
;
2. Определённый интеграл от алгебраической суммы конечного числа непрерывных функций 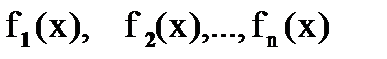 , заданных на отрезке
, заданных на отрезке 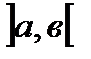 равен алгебраической сумме определённых интегралов от слагаемых функций:
равен алгебраической сумме определённых интегралов от слагаемых функций:
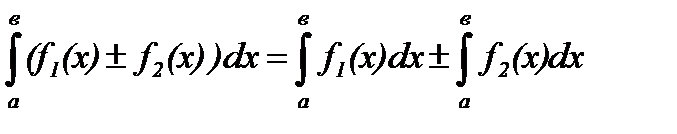 ;
;
3. Постоянный множитель можно вынести за знак интеграла:
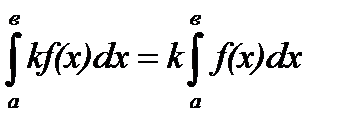 ;
; 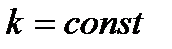
4. Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит свой знак на противоположный:
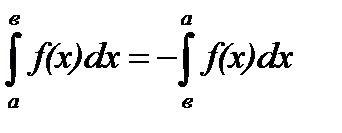 ;
;
5. Если а=в, то 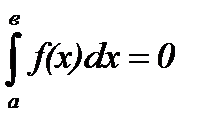 ;
;
6. Если отрезок интегрирования 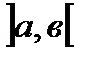 разбить на две части
разбить на две части 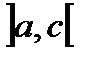 и
и 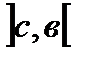 , то:
, то:
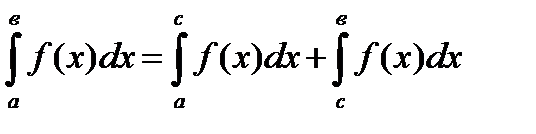 ;
;
7. Если подинтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, т.е. если 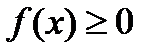 , то
, то
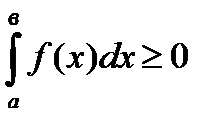 ;
;
8. Значение определённого интеграла заключено между произведениями наибольшего и наименьшего значений подинтегральной функции на длину интервала интегрирования:
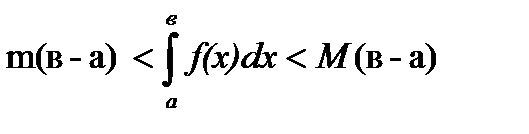 , где M,m – наибольшее и наименьшее значения функции
, где M,m – наибольшее и наименьшее значения функции 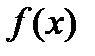 на отрезке
на отрезке 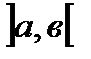 : m £
: m £ 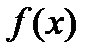 £ M.
£ M.
9. Определённый интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=С отрезка интегрирования 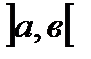 на длину отрезка (в-а):
на длину отрезка (в-а):
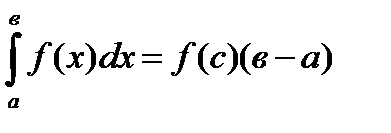 ,
,
где f(c) - среднее значение функции в интервале.
Дата добавления: 2016-06-05; просмотров: 2014;











