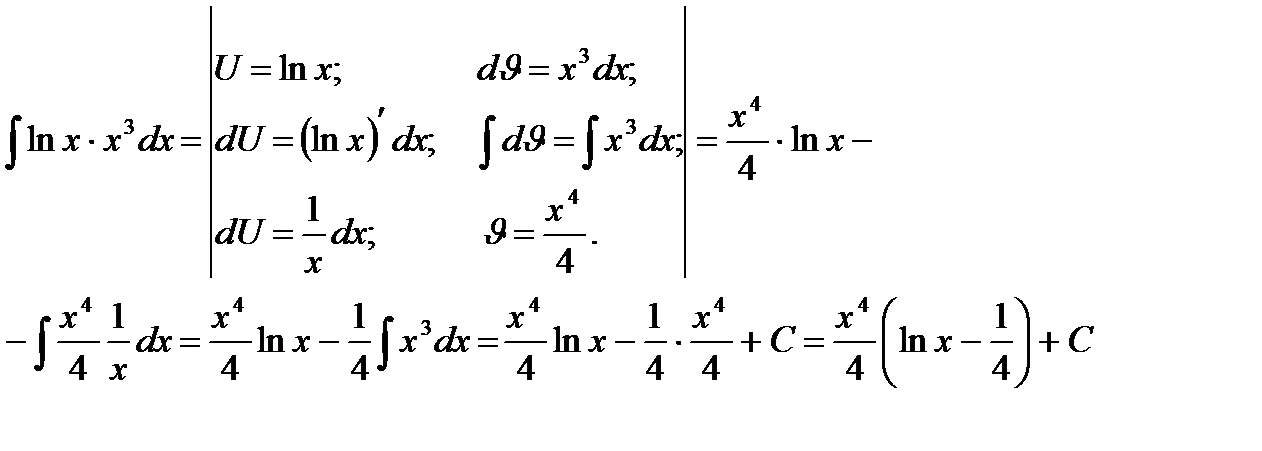Метод непосредственного интегрирования
Метод непосредственного интегрирования основан на преобразовании подинтегральной функции, применении свойств неопределённого интеграла и приведении подинтегрального выражения к табличной форме.
Например:
1) 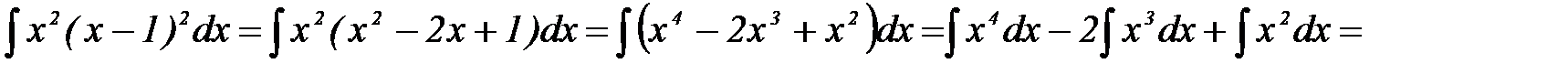
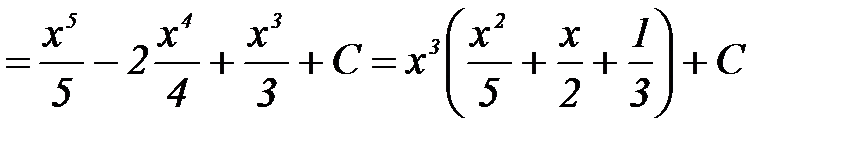
Проверка(на основании свойства №2 неопределённого интеграла):
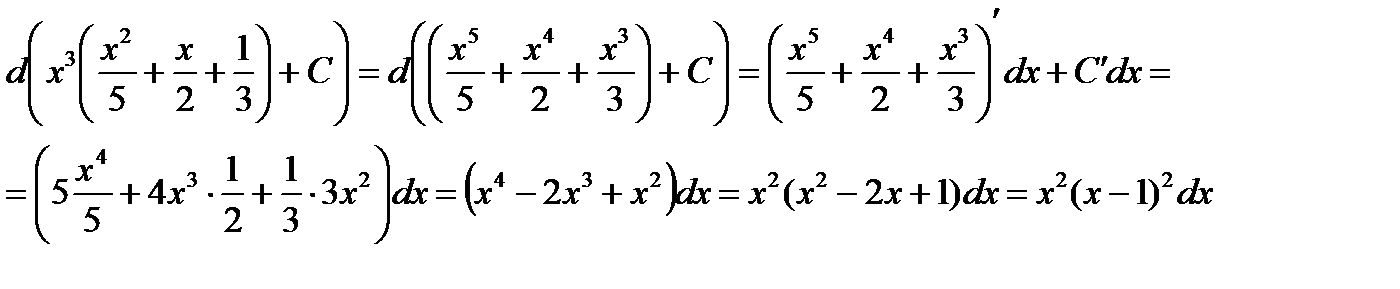
2) 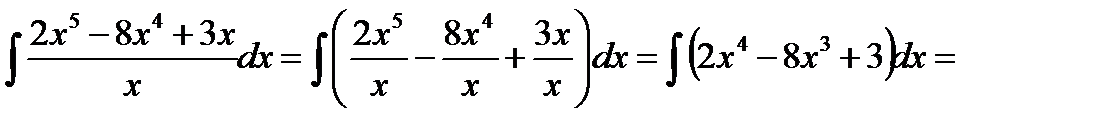
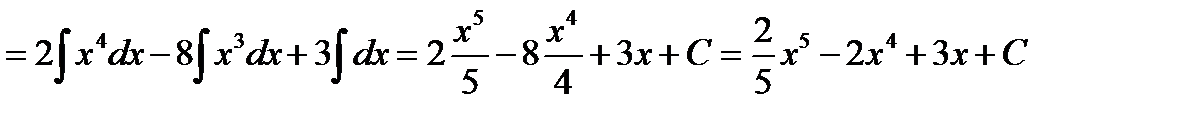
Проверка(на основании свойства №1 неопределённого интеграла): 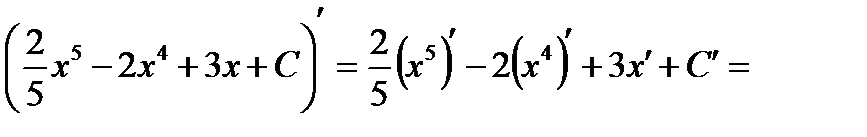
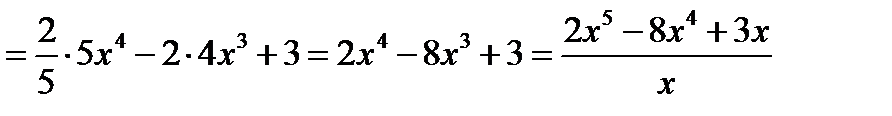
2. Метод подстановки (замены переменной)
Этот метод основан на введении новой переменной. В интеграле 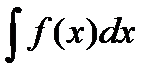 сделаем подстановку:
сделаем подстановку:
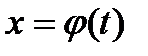 , тогда
, тогда
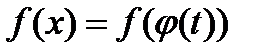 ;
;
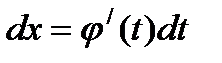 ;
;
Следовательно, получим:
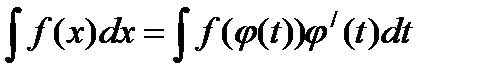
Например:
1) 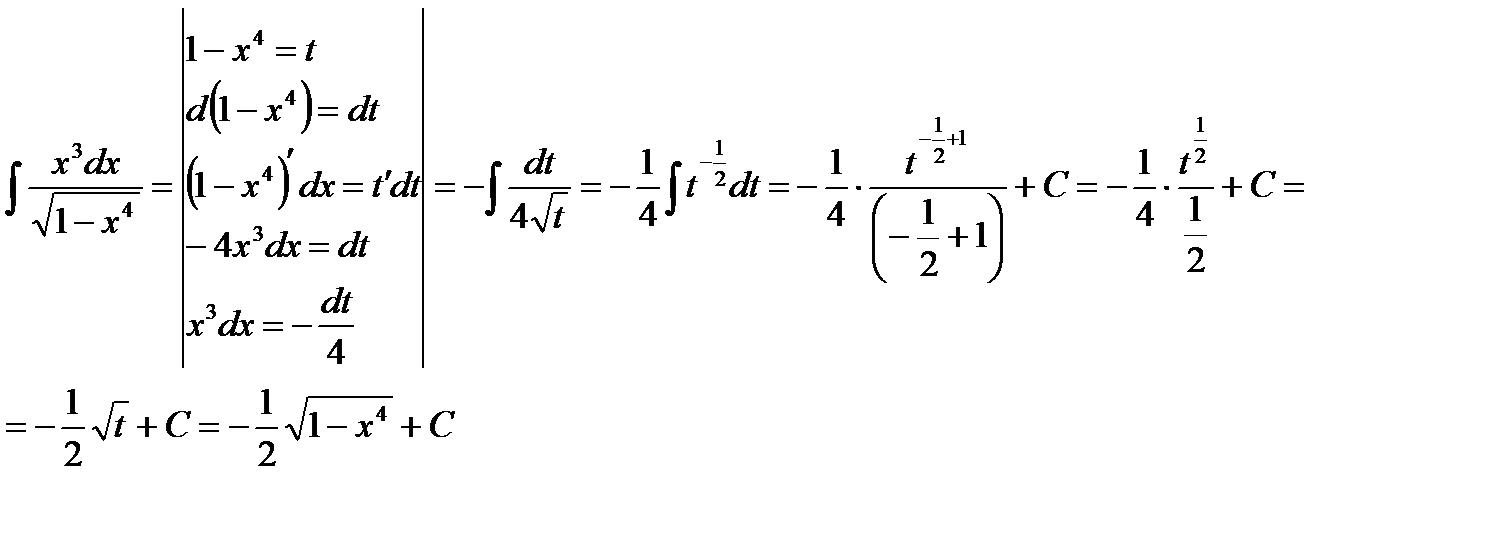
Проверка: 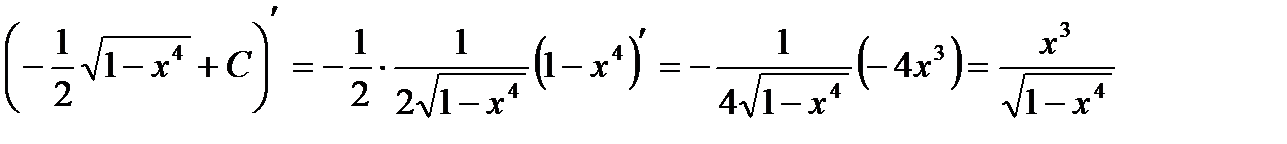
2) 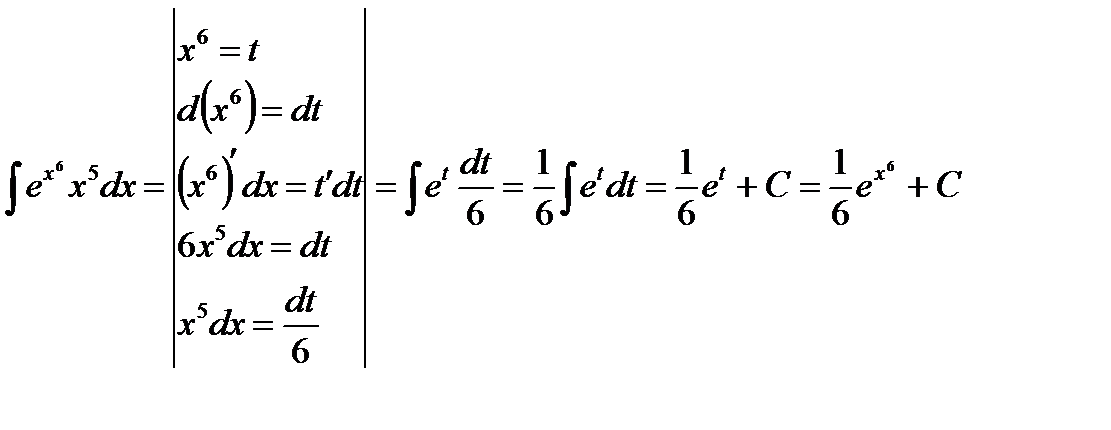
Проверка(на основании свойства №2 неопределённого интеграла):
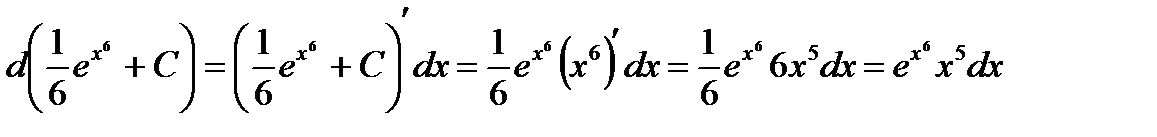
Интегрироване по частям
Пусть u иv - дифференцируемые функции. Раскроем дифференциал произведения этих функций:
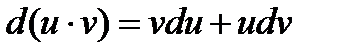 ,
,
откуда 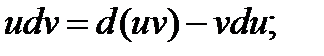
Проинтегрируем полученное выражение:
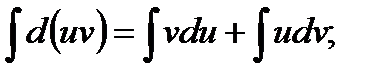
Тогда
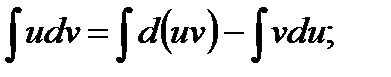
или
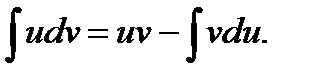
Например:
Проверка(на основании свойства №1 неопределённого интеграла):
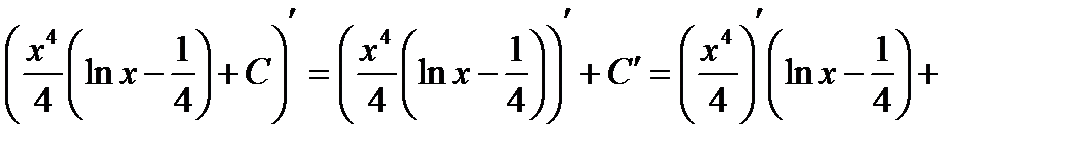
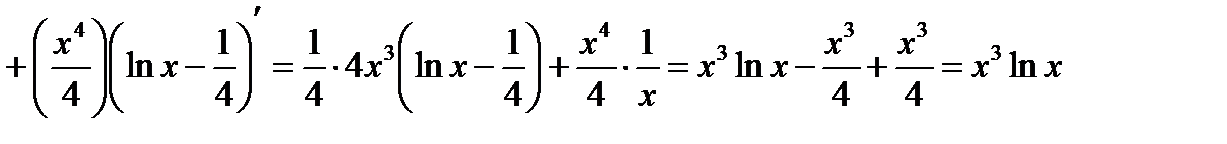
2) 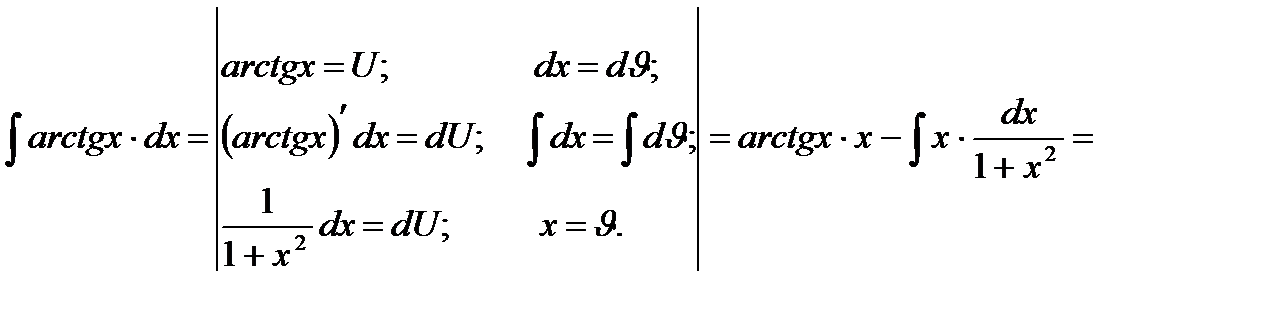
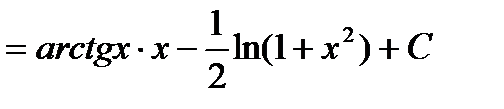
Решаем 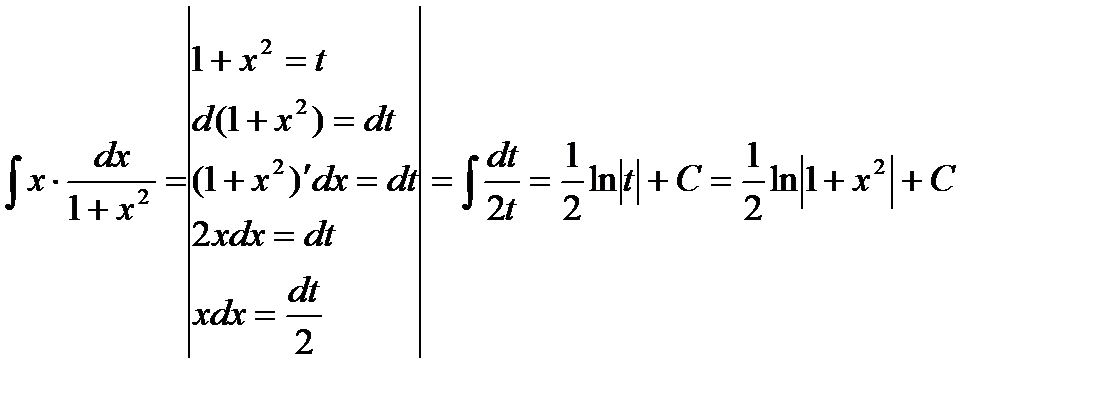
Проверка(на основании свойства №1 неопределённого интеграла):
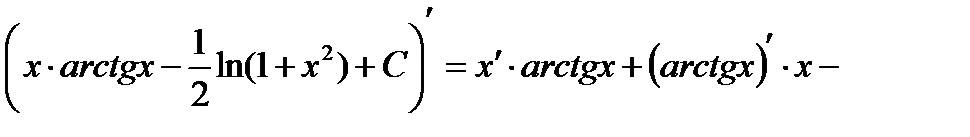
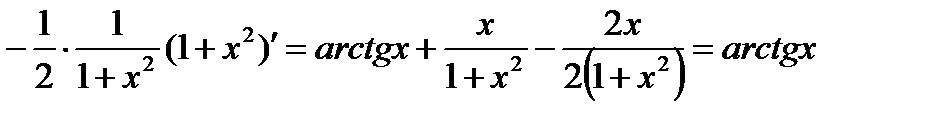
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задачи для домашнего решения
Найти интеграл:
I. Метод непосредственного интегрирования
а) 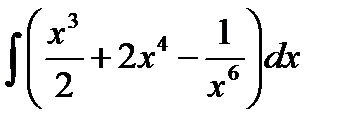 ; е)
; е) 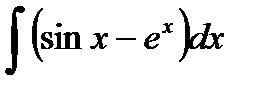 ;
;
б) 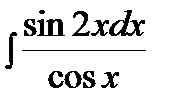 ; ж)
; ж) 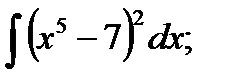
в) 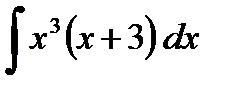 ; з)
; з) 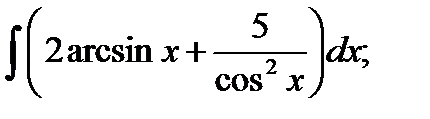
г) 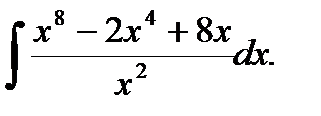 ; и)
; и) 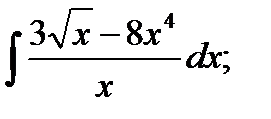
д) 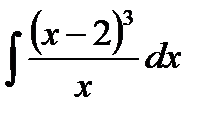 ; к)
; к) 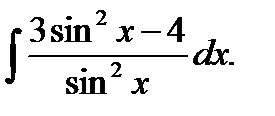
Дата добавления: 2016-06-05; просмотров: 1796;