ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ

Рассмотрим задачу о нахождении площади криволинейной трапеции.

Пусть дана некоторая функция y=f(x), график которой изображён на рисунке.

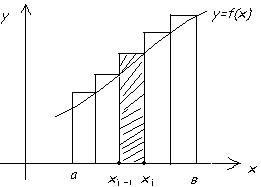
Рис 1. Геометрический смысл определенного интеграла.

На оси 0х выберем точки “a”и “в” и восстановим из них перпендикуляры до пересечения с кривой. Фигура ограниченная кривой, перпендикулярами и осью 0х называется криволинейной трапецией. Разобьём интервал 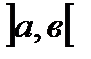на ряд небольших отрезков. Выберем произвольный отрезок 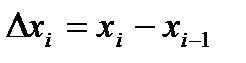. Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:

.

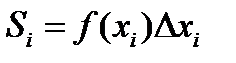Тогда площадь всех достроенных прямоугольников в интервале 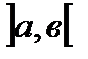будет равна:

;

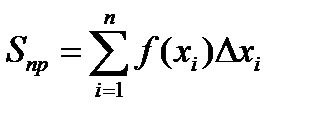Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:

;

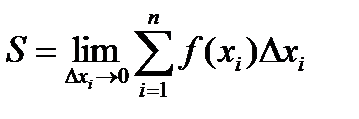Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.

Интегральная сумма есть сумма произведений приращения аргумента на значение функции f(x), взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.

Функция f(x) в некотором интервале от х=адо х=в интегрируема, если существует такое число, к которому стремится интегральная сумма при Dх®0. В этом случае число J называют определённым интегралом функции f(x) в интервале :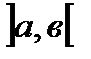

;

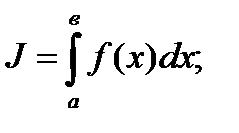
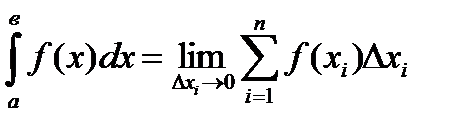где ]а, в[ – область интегрирования,

а–нижний предел интегрирования,

в–верхний предел интегрирования.

Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале ]а, в[ и осью абцисс.