ОСНОВНЫЕ МЕТОДЫ НАХОЖДЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Метод непосредственного интегрирования

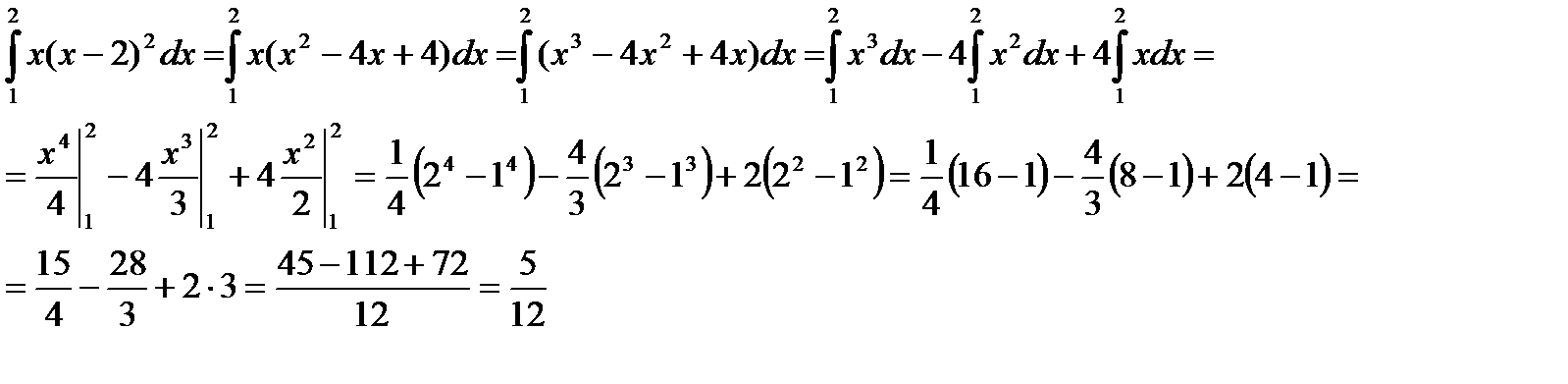
Метод подстановки

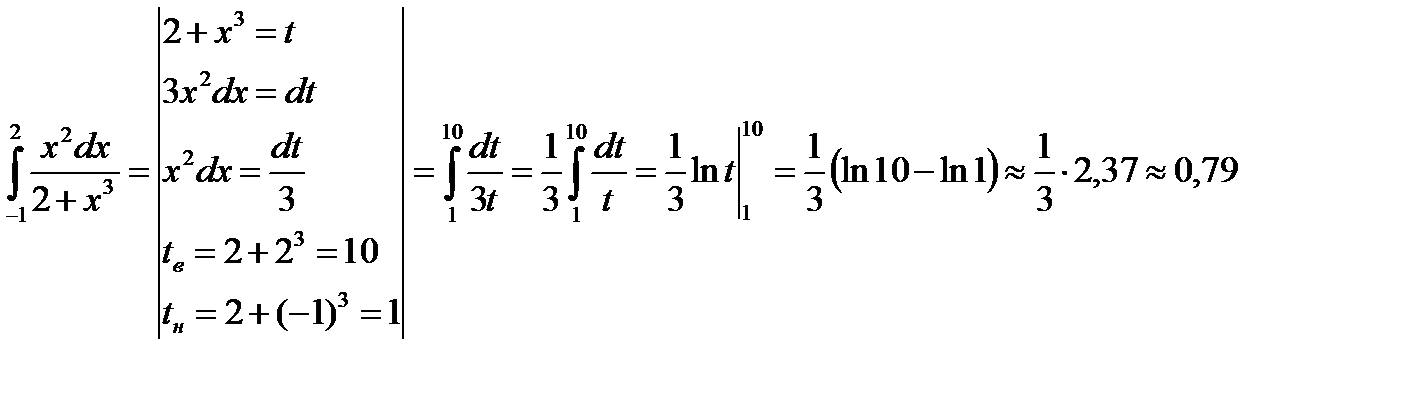
Примечание: При вычислении интеграла методом постановки переходим к новым пределам интегрирования для переменной t.

Метод интегрирования по частям

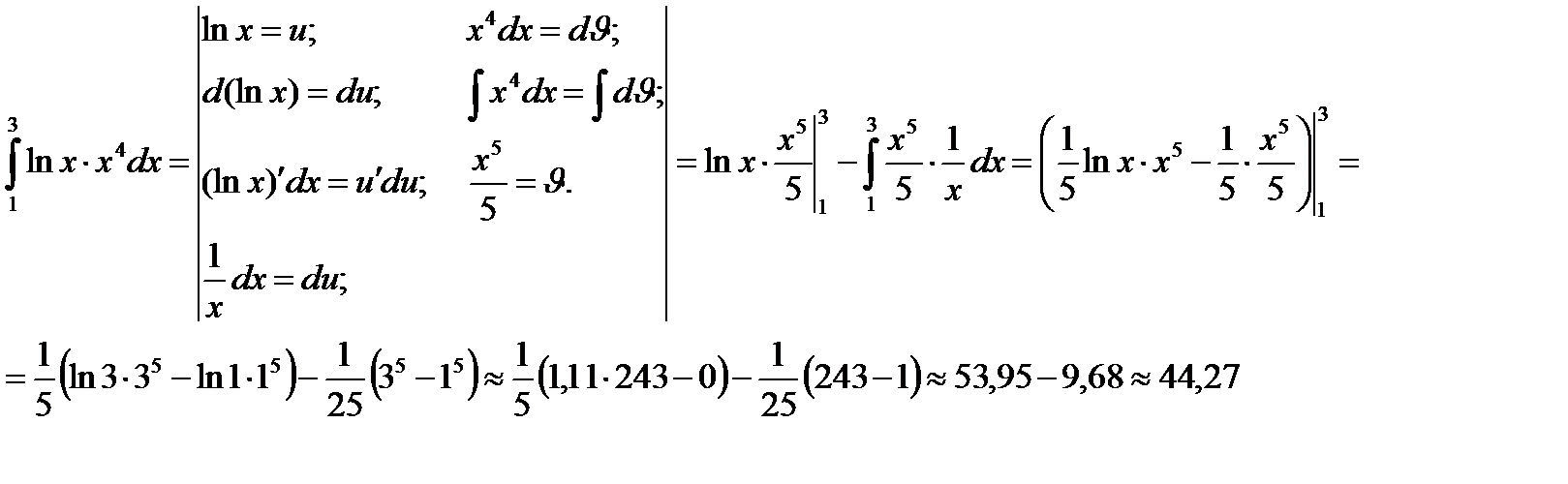
Вычисление площадей фигур, ограниченных линиями, уравнения которых заданы

Например: Вычислить площадь фигуры, ограниченную линиями:

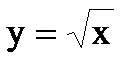и .

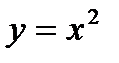Решение: Представим искомую площадь графически.

Искомая площадь площадь фигуры ОАСВ – заштрихована.

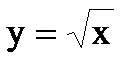
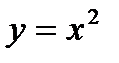
х

у

А

В

С

Д

Находим точки пересечения линий: 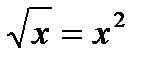, откуда x⁴ –x=0или х(х³ – 1)=0. Следовательно, абсциссы точек пересечений линий х₁=0, х₂=1, а сами точки пересечения имеют координаты (0,0) и (1,1).

В соответствии с геометрической интерпретацией определённого интеграла, определённый интеграл функции 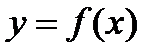в пределах от х=х₁ до х=х₂, т.е. 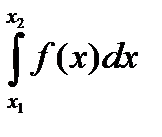, численно равен площади криволинейной трапеции, ограниченной линией графика функции y=f(x), осью абсцисс и линиями x=x₁ и x=x₂. Искомая площадь S_OACB равна разности площадей криволинейных трапеций:

.

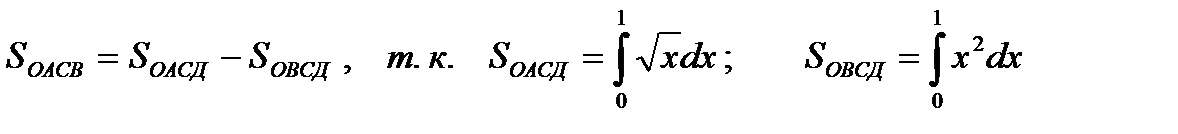Искомая площадь: 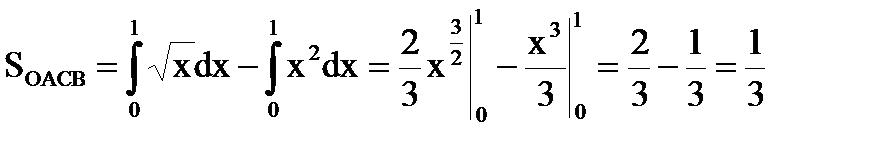(кв. ед).

Ответ: Искомая площадь равна 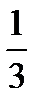(квадратных единиц).