ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ И МЕТОД ИХ РЕШЕНИЯ
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
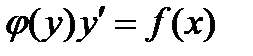
Общее решение дифференциального уравнения с разделяющимися переменными даётся формулой:
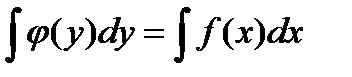 .
.
Эта формула задаёт y как функцию x неявно. Если уравнение решить относительноy, то получим явное решение дифференциального уравнения.
Пусть задано дифференциальное уравнения с разделяющимися переменными:
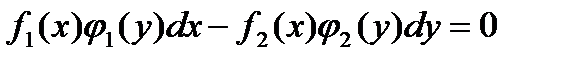 ;
;
Нужно разделить переменные: в левой части уравнения собрать все у и дифференциал dу, в правой части все х и дифференциал dx.
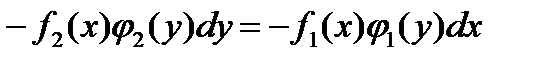 ;
;
Умножаем обе части на (-1), получаем:
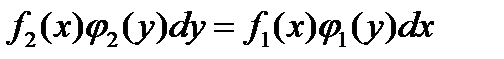 ;
;
Левую часть нужно избавить от 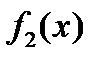 , а правую часть – от
, а правую часть – от 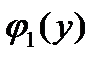 . Для этого обе части делим на
. Для этого обе части делим на 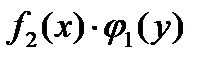 и получаем:
и получаем:
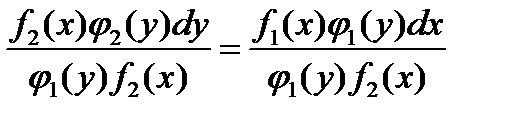 ;
;
После сокращения получим уравнение с разделенными переменными:
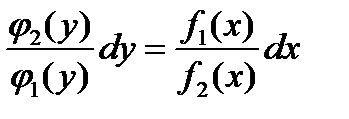 ;
;
После чего интегрируем обе части уравнения:
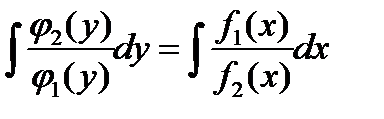 .
.
Например: Найти общее и частное решения дифференциального уравнения:
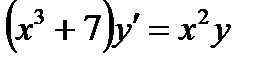 при
при 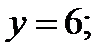 и
и 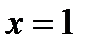 (начальные условия)
(начальные условия)
Заменяем 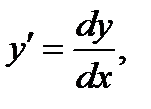 получаем:
получаем:
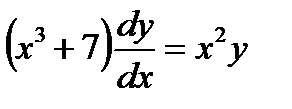 ;
;
Левую часть освобождает от х, для чего обе части умножаем на 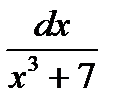
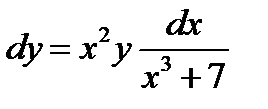 ;
;
Правую часть освобождаем от у, деля обе части на у:
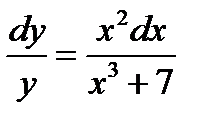 ;
;
Получили уравнение с разделенными переменными, берем интегралы левой и правой части, получаем:
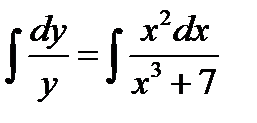
Левый интеграл табличный, а правый решаем методом подстановки.
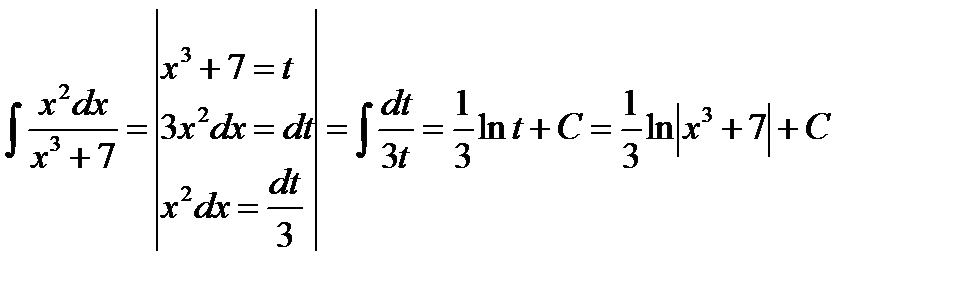 ;
;
Раскрываем оба интеграла:
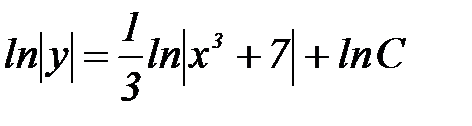 ;
;
Для удобства постоянную интегрирования С берем под знак логарифма.
Потенцируем и получаем:
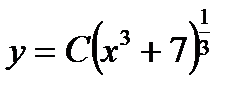 , или
, или 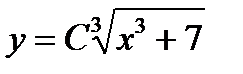 - это есть общее решение дифференциального уравнения.
- это есть общее решение дифференциального уравнения.
Находим частное решение. Для этого в общее решение подставляем начальные условия у и х и находим численное значение С:
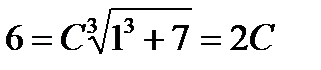 , откуда
, откуда 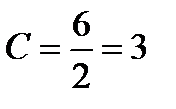
Полученные значение С подставляем в общее решение и получаем:
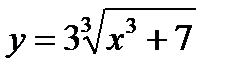 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Проверка (основана на определении, что решением дифференциального уравнения называется всякая функция, при подстановки которой и её производных в уравнение получаем тождество): 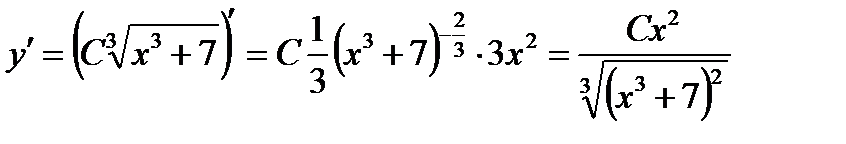 ;
;
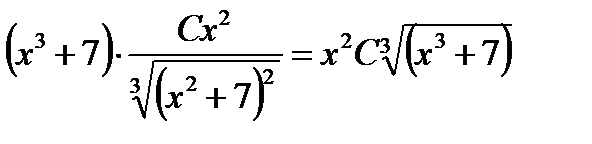 ;
;
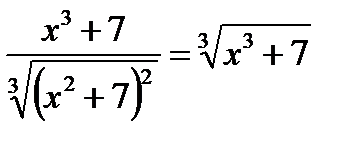 ;
;
Возводим обе части в куб:
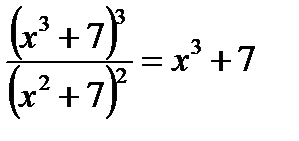 ;
;
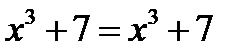 .
.
Примечание. Основные случаи потенцирования:
1. 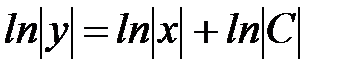
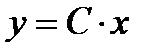 ;
;
2. 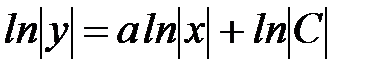
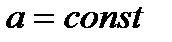
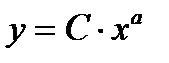 ;
;
3. 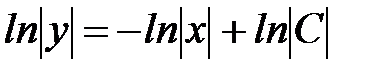
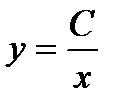 ;
;
4. 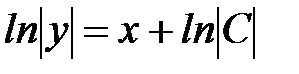
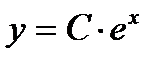 .
.
Дата добавления: 2016-06-05; просмотров: 2016;











