Предмет математической статистики.

Исходным материалом для любого статистического исследования являются статистические данные. Под статистическими данными понимаются сведения о числе объектов, какой либо обширной совокупности, обладающих теми или иными признаками (число девочек, родившихся в 1990 г.)

На основании статистических данных можно сделать определённые научно обоснованные выводы. Для этого статистические данные должны быть предварительно определённым образом систематизированы и обработаны.

Нередко возникает необходимость сравнить между собой две или несколько совокупностей статистических данных. Для проведения сравнения нужны показатели, характеризующие то или иное свойство совокупности данных одним числом. Такие показатели получили название числовых характеристик.

Простейшими числовыми характеристиками являются характеристики положения: среднее значение, мода и медиана.

Среднее значение ряда наблюдений 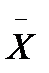- это центр рассеивания наблюдаемых значений, это расчетное значение, сумма отклонений всех вариант от которого равна 0.

Если варианты в ряду х_i являются значениями непосредственно наблюдаемого (первичного) признака, то среднее значение ряда находят по формуле среднего арифметического:

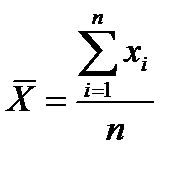(формула простой средней)

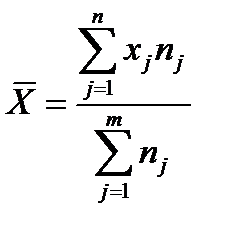(формула средней взвешенной)

МодаМ₀ – это значение вариант, встречающихся в ряду чаще всего.

Статистический ряд может иметь одну, две или несколько мод, может не иметь моды.

Медиана Ме – это срединное в вариационном ряду значение. Если число членов ряда нечетное, то медиана – это среднее число ряда.

Если n четное число, то медиана есть среднее арифметическое двух средних значение ряда.

Простейшими характеристиками рассеивания являются размах, выборочная дисперсия, выборочное отклонение.

Одним из основных методов обработки статистических данных является выборочный метод.

Выборочный метод

При выборочном исследовании из всей совокупности отбирают некоторым образом определённое число объектов и только их подвергают исследованию.

Совокупность всех исследуемых объектов называют генеральной совокупностью.

Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности.

Число объектов выборки или генеральной совокупности называют объемом выборки (из 10000 студентов для контрольной флюорографии отобрано 100 студентов, то объем генеральной совокупности равен 10000, а объем выборки равен 100).

Разность между наибольшим и наименьшим значением числовой выборки называют размахом выборки.

Выборку, представляющую собой неубывающую последовательность чисел, называют вариационным рядом. Любую числовую выборку можно записать в виде вариационного ряда.

Пример:

выборка: 1,10,-2,0,-2,5,1,10,7.

вариационный ряд: -2,-2,0,1,1,5,7,10.

объем выборки: n=8

размах выборки: 10-(-2)=12

Пусть из генеральной совокупности получена выборка объема n, причем 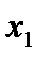появляется в ней 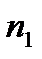раз, значение 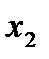- 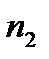раз и т.д. В этом случае числа 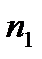, ,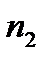…., 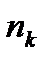называют частотами значения выборки. Отношения 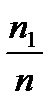, ,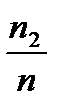…., 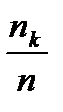называют относительными частотами значения выборки

+ +….+ =

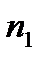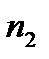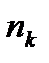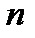
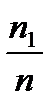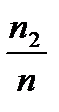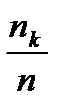+ +…. + =1

Последовательность пар ( 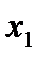, 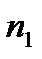), ( , 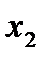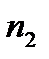), … ,( 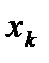, 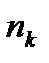), называют статистическим рядом.

Обычно статистический ряд записывают в виде таблицы, где x- значения выборки, а n- частоты значения выборки.

		…….
		…….

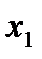
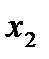
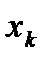
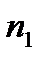
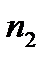
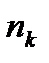
Выборочное распределение записывается в виде таблицы, где 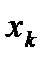- значения выборки, а 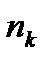относительные частоты значения выборки.

		……..
		……..

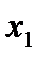
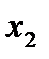
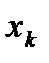
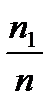
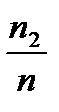
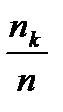
Пример:

Дана выборка 3, 8, -1, 3, 0, 5, 3, -1, 3, 5.

Запишем данную выборку в виде вариационного ряда: -1, -1, 0, 3, 3, 3, 3, 5, 5, 8.

Статистический ряд будет иметь вид:

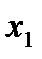
	-1

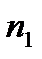
Выборочное распределение имеет вид:

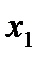
	-1
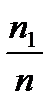
	0,2	0,1	0,4	0,2	0,1

Выборочная дисперсия D_выб.(Х) есть среднее значение квадратов отклонений всех вариант от среднего ряда :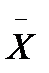

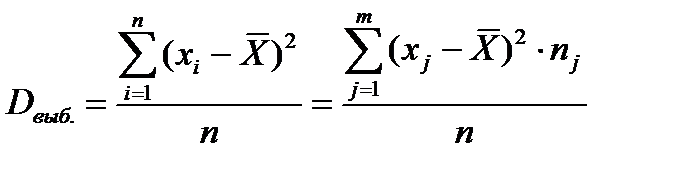
Для практических расчетов удобнее формула: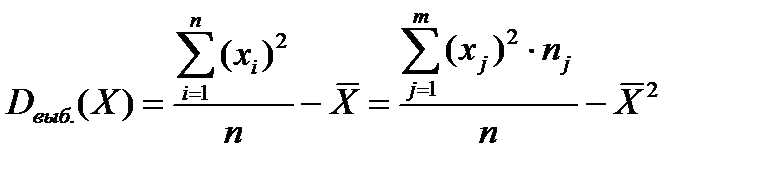

Дисперсия имеет размерность квадрата наблюдаемой величины, поэтому на практике широко используется еще один показатель рассеивания – среднее квадратичное отклонениеσ_выб.(Х): σ_выб.(Х) =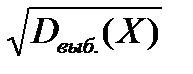

Важно помнить о принципиальном отличии числовых характеристик в теории вероятности от числовых характеристик в статистике.

В статистике числовые характеристики являются функциями результатов наблюдений, по которым они вычисляются. Бросим кубик 12 раз, найдем среднее арифметическое выпавших чисел, получим значение среднего 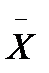₁. бросим еще раз, найдем уже другое среднее 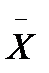₂ и т. д.Таким образом, средние величины будут колебаться и сами служить случайными величинами. В статистике эти величины рассматриваются как точечные оценки неизвестного среднего всей генеральной совокупности .

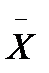Выборочный метод – метод статистического обследования, при котором из совокупности выбирают ограниченное число объектов и их подвергают изучению.

Он применяется тогда, когда количество объектов велико или сплошное обследование невозможно в силу того, что обследование может привести к уничтожению объекта (например, чтобы узнать качество консервов, банку надо вскрыть), т.е. когда не хотят проводить полное обследование объекта.

Примером сплошного наблюдения является изучение успеваемости студентов администрацией вуза, перепись населения, охватывающая все население страны. Выборочными наблюдениями являются, например, социологические исследования, охватывающие часть населения.

Выборочный метод исследования является единственно возможным в случае бесконечной генеральной совокупности или в случае, когда исследование связано с уничтожением наблюдаемых объектов. Кроме того он позволяет существенно экономить затраты ресурсов. Недостатком его является появление ошибок исследования, (их называют ошибками репрезентативности), которые связаны с тем, что изучается только часть объектов. Математическая статистика дает рекомендации, как организовать исследование, чтобы свести эти ошибки к минимуму, и дает методику оценки этих ошибок.

Для того, чтобы выборка давала представление о генеральной совокупности, необходимо, чтобы соблюдался принцип равной возможности всем элементам генеральной совокупности быть отобранными в выборку.

Выборка называется репрезентативной(представительной), если она достаточно хорошо воспроизводит генеральную совокупность, т.е. это выборка, которая производится так, что все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

Существуют специальные приемы отбора, обеспечивающие репрезентативность выборки. Опишем простейшую схему получения репрезентативной выборки из конечной, не очень большой генеральной совокупности.

Все объекты генеральной совокупности нумеруют, номера записывают, карточки перемешивают и выбирают одну наугад. Объект, номер которого совпал с номером карточки, считается попавшим в выборку. Операцию повторяют, пока не наберется нужный объем выборки. При этом, если случайно отобранная карточка возвращается обратно в общую совокупность и, следовательно, раз отобранный в выборку объект может быть отобран повторно, то имеет место выборка повторная, или выборка с возвратом.

Если же отобранная карточка и, следовательно, отобранный в выборку объект назад не возвращался, то существует выборка бесповторная или выборка без возврата.