Дисперсия случайной величины.

Цели: создание благоприятных условий для введения понятия случайных событий;

познакомить с законом распределения случайных величин; познакомить с важными характеристиками случайных величин: математическое ожидание, дисперсия, среднее квадратичное отклонение.

Ход занятия:

Если каждому элементарному событию А из некоторого множества событий 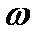можно поставить в соответствие определенную величину Х = Х(А), то говорят, что задана случайная величина.

Случайную величину Х можно рассматривать как функцию события А с областью определения .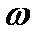

Случайная величина может принять то или иное значение из некоторого числового множества, однако заранее неизвестно, какое именно. Случайные величины принято обозначать большими буквами Х, Y, .., а принимаемые ими значения - соответствующими строчными буквами х, у,.. .

Конечный или бесконечный ряд чисел называется дискретным, если каждому числу х_n из этого ряда можно сопоставить промежуток (а_n, b_n) (a_n<x_n<b_n), внутри которого других чисел данного ряда нет.

Если значения, которые может принимать данная случайная величина Х, образуют дискретный (конечный или бесконечный) ряд чисел х₁, х₂,…, х_n, …, то и сама случайная величина называется дискретной.

Если же значения, которые может принимать данная случайная величина Х, заполняют целый конечный или бесконечный промежуток (А,В) числовой оси Ох, то случайная величина называется непрерывной.

Каждому значению случайной величины дискретного типа х_n отвечает определенная вероятность р_n; каждому промежутку (а,b) из области значений случайной величины непрерывного типа также отвечает определенная вероятность Р(а<X<b) того, что значение, принятое случайной величиной, попадает в этот промежуток.