Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Закон распределения дискретной случайной величины обычно задается рядом распределения:
| Хi | Х1 | Х2 | Х3 | …. | Хn |
| pi | P1 | P2 | P3 | …. | pn |
При этом 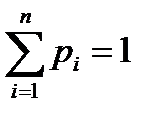 , где суммирование распространяется на все (конечное и бесконечное) множество возможных значений данной случайной величины Х.
, где суммирование распространяется на все (конечное и бесконечное) множество возможных значений данной случайной величины Х.
Закон распределения непрерывной случайной величины удобно задавать при помощи так называемой функции плотности вероятности f(x). Вероятность
Р (а<X<b) того, что значение, принятое случайной величиной Х, попадает в промежуток (а,b), определяется равенством
Р (а<X<b) = 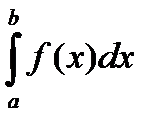 .
.
График функции f(x) называется кривой распределения.
Геометрически вероятность попадания случайной величины в промежуток (а,b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х = а, х = b.
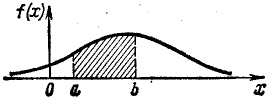
|
Функция плотности вероятности f(x) обладает следующими свойствами:
1) f(x) ≥0, 2) 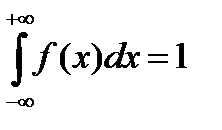
(если все значения случайной величины Х заключены в промежутке (А,В), то последнее условие может быть заменено условием 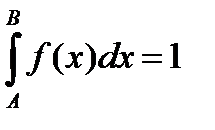 ).
).
Рассмотрим теперь функцию F(x) = Р(Х<x). Эта функция называется функцией распределения вероятности случайной величины Х.
Функция F(x) существует как для дискретных, так и для непрерывных случайных величин. Если f(x) – функция плотности распределения вероятности непрерывной случайной величины Х, то
F(x) = 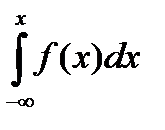 .
.
Из последнего равенства следует, что f(x) = 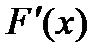 .
.
Иногда функцию f(x) называют дифференциальной функцией распределения вероятности, а функцию F(x) – интегральной функцией распределения вероятности.
Отметим важнейшие свойства функции распределения вероятности:
1) F(x)- неубывающая функция своего аргумента,
2) F (- ∞) = 0.
3) F (+∞) =1
1. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений.
Если случайная величина X характеризуется конечнымрядом распределения:
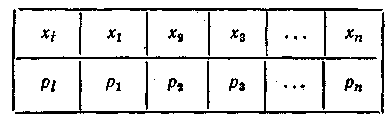 ,
,
то математическое ожидание М (X) определится по формуле
M(X) = x1p1+-x2 p2+...+xn pn, или
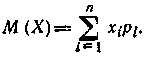
Понятие математического ожидания распространяется и на непрерывную случайную величину.
Пусть f(x) — плотность вероятности случайной величины X. Тогда математическое ожидание непрерыв ной случайной величины X определяется равенством
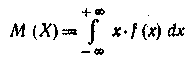
(при условии, что значение этого интеграла конечно).
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: 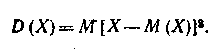
Дисперсия случайной величины есть мера рассеяния ее значений около ее математического ожидания.
Само слово дисперсия означает «рассеивание».
Если ввести обозначение М (Х) = т, то формулы для вычисления дисперсии примут следующий вид:
а)для дискретной случайной величины X:
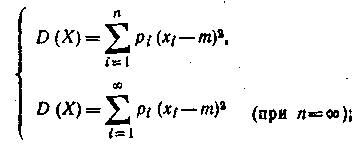
б) для непрерывной случайной величины X:
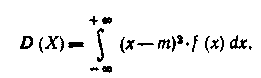
Дата добавления: 2016-06-05; просмотров: 2672;











