Если элемент х можно выбрать k способами, а элемент у – m способами, то пару (х,у) можно выбрать km способами.

Это правило носит название правила произведения. Оно же справедливо и для тройки, четверки и т.д. элементов.

Определение:произведение подряд идущих первых n натуральных чисел обозначают n! И называют «эн факториал»: n! = 1·2·3·…·(n – 1) ·n.

По-английски одно из значений слова «factor» - «множитель». Так что «эн факториал» примерно приводится как «состоящий из n множителей». Приведем несколько первых значений для n!:

Перестановки.

Пусть А – некоторое конечное множество, состоящее из n различных элементов:

А = {а₁, а₂, а₃, …, а_n}. Будем образовывать из этих элементов новые упорядоченные множества. В качестве первого возьмем множество, в котором элементы расположены в порядке возрастания их номеров (а₁, а₂, а₃, …, а_n). Второе множество можно образовать, поменяв местами элементы а₁ и а₂, а все остальные первого множества оставив на своих местах: (а₂,а₁,а₃, …, а_n). Аналогично можно строить и другие упорядоченные множества.

Всевозможные конечные упорядоченные множества, содержащие nразличных элементов, которые можно получить из некоторого неупорядоченного множества, состоящего из n различных элементов, называются перестановками из n элементов.

Перестановка есть не что иное, как способ упорядочивания элементов некоторого конечного множества.

Число перестановок из n элементов (которое обычно обозначают Р_n) равно произведению n последовательных натуральных чисел, начиная с единицы.

Это произведение имеет специальное название n! (читается: n факториал):

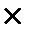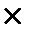Р_n = 1 2 3….(n – 1)n = n!

Пустое множество можно упорядочить только одним способом;

поэтому 0! = 1.

Размещения.

Пусть дано некоторое конечное множество А, состоящее из n различных элементов. Выберем некоторым образом из n элементов m различных элементов, и

будем составлять из этих m элементов различные упорядоченные множества.