Начальные понятия о графах

Граф и его элементы. Граф G=(V,E) определяется как совокупность двух (как правило, конечных) множеств: множества V точек, называемых вершинами, и множества E линий, соединяющих точки, называемых ребрами. Каждое ребро может быть инцидентно (присоединено к) ровно двум вершинам. Это позволяет задавать ребра парами инцидентных ему вершин. Если ребра определяются как упорядоченные пары вершин, то граф называется ориентированным графом (орграфом); ребра в этом случае называют дугами; первую вершину пары называют началом дуги и считают, что из нее дуга выходит, а вторую - концом дуги и считают, что в нее дуга заходит. Если же порядок вершин в парах, описывающих ребра графа, не имеет значения, граф называют неориентированным графом (неорграфом). Вершины, соединенные ребром или дугой, называют смежными вершинами.

Изображение и виды графов. Графически вершины графа обычно изображают точками или окружностями, а ребра - соединяющими их линиями. Направленность дуг в ориентированных графах указывают стрелками. Мы будем изображать вершины как точками, так и окружностями с надписями, когда будет возникать необходимость различать вершины между собой. На рис. 1.1 представлены различные примеры графов, неориентированных и ориентированных, иллюстрирующих некоторые понятия о графах и разновидности графов.

Если множество E ребер графа пусто (рис. 1.1, а), граф называется пустым. Если пусто не только множество E ребер, но и множество V вершин графа, граф называется нуль-графом. Пустой граф, имеющий лишь одну вершину, называется тривиальным графом.

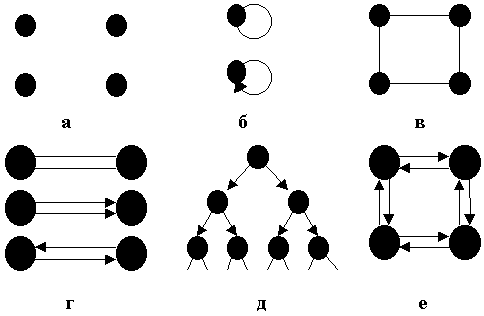
Рис. 1.1. Примеры графов различного типа

Ребро графа, соединяющее вершину саму с собой, называют петлей. Петля, как и всякое другое ребро, может быть ориентированной или неориентированной (рис. 1.1, б).

Одной и той же паре вершин в графе может быть инцидентно несколько ребер (рис.1.1, г). Такие ребра называют кратными, а граф, содержащий кратные ребра, часто называют мультиграфом. В ориентированном графе дуги считаются кратными, если они однонаправленны.

Граф не содержащий петель и кратных ребер (рис. 1.1, в), называют простым. Такой же смысл вкладывается в этот термин в случае ориентированных графов (рис. 1.1, д и рис. 1.1, е).

Обычно рассматривают конечные графы, но иногда приходится рассматривать и бесконечные графы (как, например, на рис. 1.1, д). В этом случае граф определяется некоторой процедурой или правилом порождения бесконечных множеств его вершин и ребер.

Принято считать, что неориентированному графу соответствует ориентированный граф с тем же множеством вершин, в котором каждое неориентированное ребро исходного графа заменено двумя противоположно направленными дугами. Такое соответствие между неорграфом и орграфом называют каноническим (каноническим представлением графа на рис. 1.1, в является граф на рис. 1.1, е). Граф может содержать одновременно как ребра, так и дуги. Получение канонического представления такого графа сводится к замене ребер двумя противоположно направленными дугами без изменения имевшихся дуг. Например, графом такого типа будет изображение вершинами населенных пунктов и развилок дорог, а ребрами и дугами – дорог, соответственно, с двусторонним и односторонним движением.