Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей.
Для двух несовместных событий А и В вероятностей этих событий равна сумме их вероятностей:
Р(А или В)=Р(А) + Р(В).
Пример №3:найти вероятность выпадения 1 ил 6 при бросании игральной кости.
Событие А (выпадение 1) и В(выпадение 6) являются равновозможными: Р(А) = Р(В) = 1/6, поэтому Р(А или В) = 1/6 + 1/6 = 1/3
Сложение вероятностей справедливо не только для двух, но и для любого числа несовместных событий.
Пример №4:в урне находится 50 шаров: 10 белых, 20 черных, 5 красных и 15 синих. Найти вероятность появления белого, или черного, или красного шара при однократной операции изъятия шара из урны.
Вероятность вынимания белого шара (событие А) равна Р(А) = 10/50 = 1/5, черного шара (событие В) равна Р(В) = 20/50 = 2/5 и красного шара (событие С) равно Р(С) = 5/50 = 1/10. Отсюда по формуле сложения вероятностей получим Р(А или В или С) = Р(А) +Р(В) =Р(С) = 1/5 + 2/5 + 1/10 = 7/10
Сумма вероятностей двух противоположных событий, как следует из теоремы сложения вероятностей, равна единице:
Р(А) + Р( 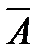 ) = 1
) = 1
В выше рассмотренном примере вынимание белого, черного и красного шара будет событием А1, Р(А1) = 7/10. Противоположным событием 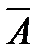 1 является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаем Р(
1 является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаем Р( 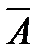 1) = 15/50 = 3/10 и Р(А) + Р(
1) = 15/50 = 3/10 и Р(А) + Р( 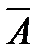 ) = 7/10 +3/10 = 1.
) = 7/10 +3/10 = 1.
Если события А1, А2, ..., Аn образуют полную систему попарно несовместных событий, то сумма их вероятностей равна 1.
В общем случае вероятность суммы двух событий А и В вычисляется как
Р(А+В) = Р(А) + Р(В) - Р (АВ).
Теорема умножения вероятностей:
События А и В называются независимыми, если вероятность появления события А не зависит от того, произошло событие В или нет, и наоборот, вероятность появления события В не зависит от того, произошло событие А или нет.
Вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий Р(А и В)=Р(А)·Р(В).
Пример: В одной урне 5 черных и 10 белых шаров, в другой 3 черных и 17 белых. Найти вероятность того, что при первом вынимании шаров из каждой урны оба шара окажутся черными.
Решение: вероятность вытаскивания черного шара из первой урны (событие А) – Р(А) = 5/15 = 1/3, черного шара из второй урны (событие В) – Р(В) = 3/20
Р(А и В)=Р(А)·Р(В) = (1/3)(3/20) = 3/60 = 1/20.
На практике нередко вероятность события В зависит оттого, произошло некоторое другое событие А или нет. В этом случае говорят об условной вероятности, т.е. вероятности события В при условии, что событие А произошло. Условную вероятность обозначают P(B/A).
Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых между собой событий. В том случае, когда событие В выполняется при условии, что событие А имело место, вероятность совместного появления двух этих событий равна
Р(А и В)=Р(А)Р(В/А).
В урне 5 шаров: 3 белых и 2 черных. Найти вероятность того, что последовательно один за другим будут вынуты черный и белый шары.
Вероятность того, что первым будет изъят черный шар (событие А), равна Р(А) = m/n = 2/5. После удаления черного шара в урне остается 4 шара: 3 белых и 1 черный. В этом случае вероятность вынимания белого шара (событие В после выполнения события А) равна Р(В/А) = ¾. Получаем Р(А и В)=Р(А)Р(В/А) = (2/5)(3/4) = 3/10.
Если событие А может произойти только с одним из событий Н1,Н2,…Нn, которые образуют полную систему попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности
Р(А) = Р(А/Н1)Р(Н1)+Р(А/Н2)Р(H2)+...+Р(А/Нn)Р(Нn).
Для вычисления вероятности P(Hi /A) в этом случае используется формула Байесa:
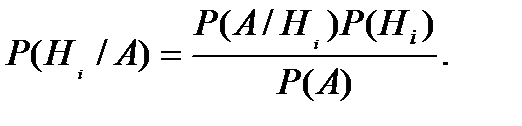
Контрольные вопросы
1.Дайте определение вероятности событий.
2.Какие события называются равновозможными?
3.Какие события называются достоверными?
4.Какие события называются невозможными?
5.Какие события называются противоположными?
6.Сформулируйте классическое определение вероятности.
7.Чему равна вероятность достоверного события? Невозможного события?
8.Назовите формулы сложения и умножения вероятностей.
Домашнее задание
Заполните в рабочей тетради занятие 11-12.
Лекция № 6
Тема: : Основные понятия теории вероятности и математической статистики
План:
Дата добавления: 2016-06-05; просмотров: 3564;











