Разложение функций в ряд Маклорена.

<13 14 151617 18 19 >

Ряд 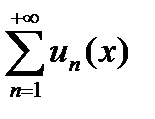= u₁(x) + u₂(x) + u₃(x) + ..., члены которого являются функциями от переменной х, называется функциональным рядом.

При различных значениях х из функционального ряда получаются различные числовые ряды, которые могут сходиться или расходиться.

Совокупность значений х, при которых функциональный ряд сходится, называется его областью сходимости.

Из всех функциональных рядов простейшими и наиболее употребляемыми являются степенные ряды вида 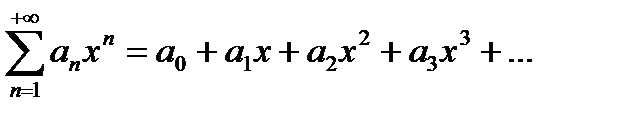или более общего вида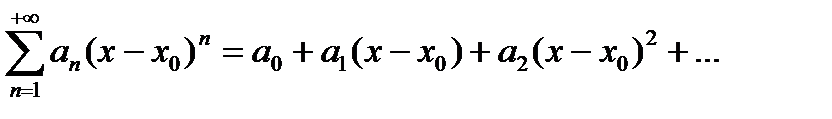

Рядом Тейлора для функции f(x) в окрестности точки а называется степенной ряд относительно двучлена х – а вида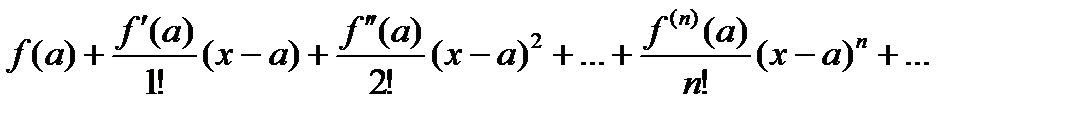

При а= 0 ряд Тейлора есть степенной ряд относительно независимой переменной х:

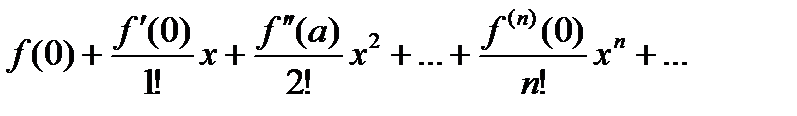
который принято называть рядом Маклорена.

Например: разложить в ряд Маклорена функцию е^х

Решение: Найдем значение данной функции при х = 0: у(0) = е⁰= 1;

Найдем значение производной данной функции при х = 0: у^/ = (е^х)^/ = е^х

у^/(0) = е⁰= 1. Подставляя эти значения в общее выражение ряда Маклорена для произвольной функции, получим ряд Маклорена для данной функции:

е^х = 1 +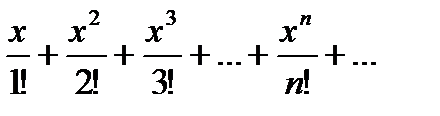

Элементы множеств

Множество можно представить себе как соединение, совокупность, собрание некоторых предметов, объединенных по какому либо признаку (множество студентов группы, множество книг на полке, множество точек на прямой и т. д.)

Элементами множества называются предметы, из которых со стоит множество (студент в группе, книга на полке, точка на прямой и т. д.)

Для обозначения и записи множеств используются заглавные буквы латинского алфавита или символическая запись (со скобками). Элемент множества обычно обозначается малой буквой латинского алфавита или конкретным знаком (рисунком): А, {х, у, z}, {A, D, 0}

Отношение принадлежности элемента некоторому множеству записывают с помощью символа е (символ £ обозначает отношение "не принадлежит").

Множество считается заданным (известным), если или перечислены все его элементы, или указано такое свойство его элементов, • которое позволяет судить о том, принадлежит ли данный элемент множеству или нет.

Множества, состоящие из одних и тех же элементов, называются равными. В этом случае используется запись А = В.

Если любой элемент множества В является и элементом множества А, то множество В называется подмножеством (частью) множества А. В таком случае говорят, что В содержится в А, пишут: В 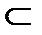А. В силу этого определения, любое множество являете* подмножеством самого себя.

Для удобства рассматривают и множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом Ø По определению, пустое множество является подмножеством любого множества.

<13 14 151617 18 19 >

Дата добавления: 2016-06-05; просмотров: 2342;